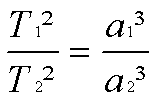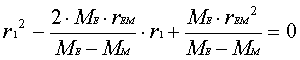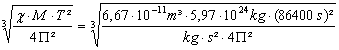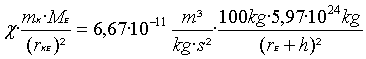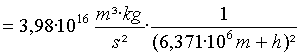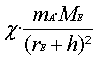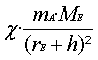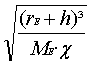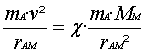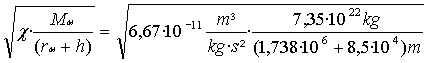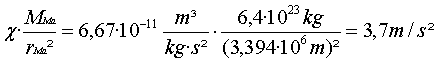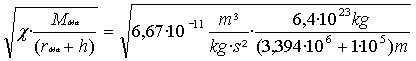Hausaufgaben - Physik Klasse 11-I GK
home
zurück
top
HA
- Einführung in die Kinematk
1.
Zwei Lastzüge fahren mit 97 bzw. 100 km/h auf der Autobahn. Der
schnellere setzt zum Überholvorgang an. Die Länge der beiden Lastzüge sei mit
18 m angegeben, der Sicherheitsabstand vor und nach dem Überholen möge 20 m
betragen.
-
Wie lange dauert der Überholvorgang?
-
Welche Strecke hat der schnellere LKW dabei zurückgelegt?
(Hinweis:
Fertigen Sie eine geeignete Skizze des Sachverhaltes an und ignorieren Sie dabei
den eigentlich notwendigen Spurwechsel!)
mit
Bezugssystemwechsel in den LKW 1 gilt: ∆v =
∆s/∆t
∆t = ∆s/∆v = 76m/(0,833m·s-1) =
91,2s
s2 = v2·∆t
= 27,78m/s ·91,2 s = 2533,33m
home Stoff
zurück Übung
top
HA
- Augenblicks- und Durchschnittsgeschwindigkeit
Aufgabe:
Ein Auto fahre von Adorf nach Bstadt mit einer konstanten
Geschwindigkeit von 60 km/h; kehrt dort sofort um und absolviert den Rückweg
mit konstanter Geschwindigkeit von 40 km/h. Berechnen Sie die
Durchschnittsgeschwindigkeit der gesamten Bewegung von Adorf nach Bstadt und
zurück! (Tipp: das richtige Ergebnis lautet nicht
50 km/h)
v
= (2·60·40)/(60+40) = 48 (km/h)
home Stoff
zurück Übung
top
HA
- Geradlinig gleichförmige Bewegung
Aufgabe:
Ein Fahrzeug legt in insgesamt 4 Stunden einen Gesamtweg
von 200 km zurück. Dabei bewegt es sich auf einer Teilstrecke s1 mit
80 km/h und auf der zweiten Teilstrecke s2 mit 40 km/h. Beide
Bewegungsabschnitte dürfen als gleichförmig angesehen werden. Berechnen Sie
die Länge der beiden Teilstrecken s1 und s2!
| s
= s1 + s2
s = v · t
t = t1
+ t2
200
= s1 + s2
s1
= v1 · t1
4 = t1
+ t2
200 = v1·t1
+ v2·t2
s2
= v2 · t2
t2 = 4 - t1
200 = 80 ·t1 + 40·(4
- t1)
200 = 80t1 + 160 - 40t1
40 = 40t1
t1 = 1(h)
t2 = 3(h)
s1 = 80·1
= 80(km)
s2 = 40·3
= 120(km) |
Geschwindigkeits-Zeit-Diagramm
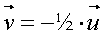
die Rechteckflächen entsprechen den Teilstrecken s1
und s2 |
Aufgabe:
Auf den Anfang eines gleichförmig bewegten Transportbandes
wird ein kleines fahrendes Spielzeugauto gesetzt. Nach
t1 = 6 s
erreicht es das Ende des Bandes. Lässt man es in die andere Richtung vom
Ende des Bandes bis zum Anfang zurückfahren, so benötigt es dafür
t2 = 26 s.
Welche Zeit t3
braucht ein auf dem
Transportband liegender Karton, um vom Anfang des Transportbandes an das Ende zu
gelangen.
|
aus v = s /
t folgt für die drei Bewegungen |
| I vA
+ vB = lB / t1 |
II vA
- vB = lB / t2 |
III
vB = lB / t3 |
| aus I - II
folgt: 2vB = lB / t1 - lB
/ t2
mit Zahlen folgt: 2vB = lB
/ 6s - lB / 26s
Erweitern auf Hauptnenner: 2vB =
(13lB - 3lB)/
78s
oder: 2vB = 10lB / 78s |
|
| nach
Einsetzen von III folgt: 2lB / t3 = 10lB / 78s
nach überkreuz ausmultiplizieren folgt:
78s · 2lB = 10 lB ·t3
nach Division mit 10 lB
folgt: t3 = 15,6 s |
Aufgabe:
Eine Fledermaus bewegt sich mit konstanter Geschwindigkeit
auf ein Hindernis zu und stößt einen Schrei aus, dessen Echo sie nach
0,145 s empfängt.
0,500 s nach Empfang des
Echos stößt sie einen zweiten Schrei aus, dessen Echo sie nach
0,101 s empfängt.
Berechnen Sie die Fluggeschwindigkeit der Fledermaus. (Die
Schallgeschwindigkeit in Luft wird mit 330
m/s angenommen.)
home Stoff
zurück Übung
top
HA
- Gleichmäßig beschleunigte Bewegung
Aufgabe:
Ein PKW nähert sich dem Ortseingangsschild einer Gemeinde
mit einer Geschwindigkeit von 80 km/h. Er kann maximal eine Bremsbeschleunigung
von -7,8 m/s2 erreichen. In welcher Entfernung vor dem
Schild muss der Fahrer den Bremsprozess spätestens beginnen, um die
vorgeschriebene Geschwindigkeit von 50 km/h am Ortseingang einzuhalten? v
= √(2·a·s + vo2)
s = (v2 - vo2)/2·a = ((13,89m/s)2 -
(22,22m/s)2)/(2·(-7,8m/s2)) = 19,29m
Ein Fahrzeug hat eine Anfangsgeschwindigkeit von 6
m/s und legt innerhalb der ersten fünf Sekunden eine Strecke von 40m
zurück. Wie groß ist seine Beschleunigung?
s = ½·a·t2 + vo·t
a = 2·(s - vo·t)/t2 =2·(40m - 6m/s·5s)/(5s)2
=0,8m/s2
Welche Beschleunigung hat ein Güterzug, der 25
Sekunden benötigt, um seine Geschwindigkeit von 36 km/h
auf 48 km/h zu erhöhen? Welche Strecke legt er dabei zurück?
v = √(2·a·s
+ vo2) a = (v2 - vo2)/2·s
= ((13,33m/s)2 - (10m/s)2)/(2·25s) = 1,56
m/s2
Ein PKW bremst mit einer Verzögerung (Bremsbeschleunigung)
von 6,5 m/s2 und legt bis zum Stillstand eine Strecke von 45 m
zurück. Wie groß sind Bremszeit und Anfangsgeschwindigkeit?
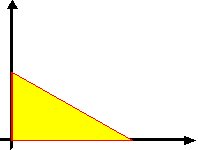
| Interpretation als gleichmäßig beschleunigte
Bewegung mit Anfangsbedingungen |
Uminterpretation als gleichmäßig beschleunigte
Bewegung aus der Ruhe |
| geg.: a = -6,5 m/s2 s = 45m v
= 0 m/s ges.: vo, t
Lösung: v = √(2·a·s
+ vo2)
vo
=√( v2
- 2·a·s) =√(02 - 2·(-6,5m/s2·45m))
=23,24m/s
v = a·t + vo
t =(v - vo)/a =(0-23,24m/s)/(-6,5m/s) =3,58s |
 |
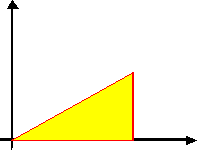
geg.: a = 6,5 m/s2 s = 45m
Lösung: v = √(2·a·s)
v =√(2·6,5m/s2·45m)
=23,24m/s
v = a·t t = v/a = (23,24m/s)/(6,5m/s2)
= 3,58s
Vereinfachung möglich. weil
beide Dreiecksflächen gleichgroß |
 |
home Stoff
zurück Übung
top
HA
- Verbundene Bewegungen
|
Ein Personenzug mit einer normalen
Reisegeschwindigkeit von 180 km/h muss innerhalb einer 3 km langen
Baustellendurchfahrt seine Geschwindigkeit auf 36
km/h drosseln. Die Brems- bzw. Anfahrbeschleunigungen vor bzw. nach der
Baustellendurchfahrt betragen -0,4 bzw. 0,2 m/s².
a) Wie viele Meter vor der Baustelle muss der Lokführer den
Bremsprozess einleiten?
s = (v2 - vo2)/2·a =
((10m/s)2 - (50m/s)2)/(2·(-0,4m/s2)) = 3000m
b) Wie viele Meter nach der Baustelle hat der Zug wieder seine
normale Reisegeschwindigkeit erreicht?
s =
(v2 - vo2)/2·a =
((50m/s)2 - (10m/s)2)/(2·(0,2m/s2)) = 6000m
c) Um wie viele Minuten verspätet sich der Zug im nächsten
Bahnhof?
tbrems = 2s/(v+vo)
= 6000m/(60m/s) = 100s tbeschl
= 2s/(v+vo) = 12000m/(60m/s) = 200s
tBaustellendurchfahrt
= s/v = 3000m/(10m/s) = 300s
also Gesamtfahrzeit bis
alte Geschwindigkeit wieder erreicht t = 600s = 10 min
und da
für die 12km ohne Baustelle gilt: t = s/v = 12000m/(50m/s) = 240s = 4 min
haben wir eine Verspätung von 10 min - 4 min = 6 min
d) Skizzieren Sie den Vorgang sowohl in einem s-t-Diagramm wie
auch in einem v-t-Diagramm!
|
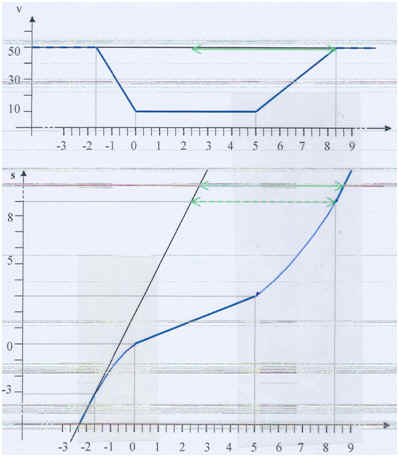
|
|
Ein Auto (A) startet bei Grün vor
einer Ampel und erreicht nach 5 Sekunden bei konstanter Beschleunigung eine
Geschwindigkeit von 60 km/h, mit der es weiterfährt. Im
Moment des Starts wird es von einem anderen Auto (B) mit einer konstanten
Geschwindigkeit von 40 km/h überholt.
a) Wie lange dauert es, bis Auto (A) so
schnell fährt wie Auto (B) ?
v = a·t
a = v/t = (16,67m/s)/(5s) = 3,33 m/s2 t = v/a =
(11,11m/s)/(3,33m/s2) = 3,33 s
b) Welchen Vorsprung besitzt zu diesem
Zeitpunkt Auto (B) vor Auto (A) ?
sB =
v·t = 11,11m/s·3,33s = 37,04m SA = ½·a·t2
= ½·3,33m/s2·3,33s = 18,52m
∆s = 18,52m
c) Welches Auto liegt am Ende des
Beschleunigungsvorganges von Auto (A) vorne? Wie
groß ist dieser Vorsprung?
sB
=11,11m/s·5s =55,56m sA =½·3,33m/s2·5s
=41,67m
Auto B liegt
immer noch vor Auto A und zwar
∆s = 13,89m
d) In welcher Zeit und in welcher
Entfernung von der Ampel holt Auto (A) das andere Auto ein? Wie
sieht der Vorgang im v-t-Diagramm und im s-t-Diagramm aus (Einteilung in m
und s)?
ab t =
5s bewegen sich beide Autos gleichförmig, aber mit unterschiedlichen
Geschwindigkeiten; es gilt:
sA
= sB + so also vA·t = vB·t
+ so daraus folgt t·(vA - vB)
= so und t = so/(vA - vB)
= 13,89m/(5,55m/s) = 2,5s
Gesamtzeit
beträgt also t = 7,5s
für
den Treffort gilt: s = vB·t = 11,11m/s·7,5s =
83,33m oder s = vA·t + so =
16,67m/s·2,5s + 41,67m = 83,33m |
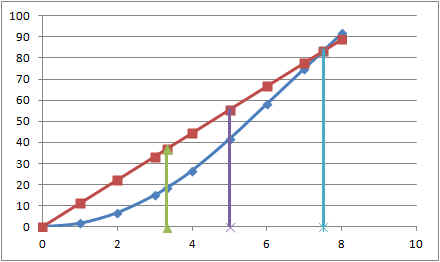
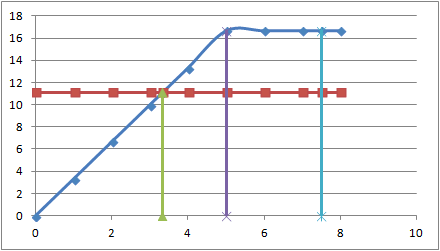
|
home Stoff
zurück Übung
top
HA
- Der freie Fall als Sonderfall gleichmäßig beschleunigter Bewegungen
- Ein
Stein fällt 4,5 s
frei herab. Wie groß ist seine Geschwindigkeit beim Aufschlagen und
welche Höhe hat er durchfallen?
v =
-44,145
m/s y = -99,33 m
- Ein
Mauerstein fällt aus 16 m
frei herab. Nach welcher Zeit und mit welcher Geschwindigkeit schlägt
er auf?
t = 1,8s v = -17,7 m/s
- Aus
welcher Höhe muss der Bär einer Ramme herabfallen, wenn er beim Aufschlag
eine Geschwindigkeit von 4,5
m/s haben soll?
y
= 1,03 m (t = 0,46 s)
Um die Tiefe eines Brunnens zu ermitteln, lässt ein Tourist einen kleinen
Stein in den Brunnen fallen. Nach 4,2 Sekunden hört er den Aufprall des
Steines auf die Wasseroberfläche. Wie tief ist der Brunnen bis zur Wasser-
oberfläche?
y = 77,5 m
home Stoff
zurück Übung
top
HA
- Überlagerte Bewegungen - das Unabhängigkeitsprinzip
home Stoff
zurück Übung
top
HA
- Der senkrechte Wurf
-
Ein Stein fällt frei aus einer Höhe von
20 m herab; ein zweiter
Stein wird vom Boden aus senkrecht hochgeworfen. Beide Vorgänge laufen
gleichzeitig ab. Mit welcher Geschwindigkeit muss der zweite Stein
hochgeworfen werden, wenn er dem ersten genau in 15 m Höhe
begegnen soll? zuerst tF = 1,43 s für
5m
freien Fall und danach voy = 14,0
m/s (aufpassen: die 15m müssen nicht zwangläufig
die Steighöhe sein!)
-
Mit welcher Geschwindigkeit muss man senkrecht nach oben
springen, um eine Höhe von 2 m zu erreichen? voy
= 6,26 m/s
-
Die Geschwindigkeit eines Weltklassesprinters beträgt etwa
10 m/s .Welche Höhe wäre damit im Hochsprung erreichbar, wenn es
dem Springer gelänge, mit dieser Geschwindigkeit senkrecht nach oben
zuspringen? Vergleichen Sie ihr Ergebnis mit dem Weltrekord im
Stabhochspringen! sh = 5,10
m
-
Wie viel Zeit vergeht, bis ein mit der
Anfangsgeschwindigkeit von 80
m/s abgeworfener Körper die Höhe von 200 m erreicht? Deuten Sie die beiden
Zahlenwerte des Ergebnisses! aus 80 =
-4,905·t2 + 80·t folgt t1 =
3,09 s und t2 = 13,21 s und beide sind sinnvoll!!
home Stoff
zurück Übung
top
HA
- Der waagerechte Wurf
- Ein Wasserstrahl tritt mit einer Austrittsgeschwindigkeit von 8 m·s-1
horizontal aus einer Düse. Mit welcher Geschwindigkeit vg
und unter welchem Winkel α gegen die Senkrechte trifft er
3 m tiefer auf eine horizontale Fläche?
v
= 11,08 m/s α
=
46,3°
- Von einem horizontalen Förderband soll Kohle bei
2,5 m Falltiefe 1,80 m
weit geworfen werden. Welche Laufgeschwindigkeit v muss das Band haben?
v = 2,52 m/s
home Stoff
zurück Übung
top
HA
- Der schräge Wurf
-
Ein unter einem Winkel von
α
= 20° aufwärts
gestelltes Förderband wirft Bauschutt mit einer Anfangsgeschwindigkeit
von vo = 2,2 m·s-1
in die 4 m
unter seinem oberen Ende stehende Lore. Wie groß ist die Wurfweite?
xW
= 2,03 m
-
Ein Geschoss wird unter einem Winkel von
30° gegenüber der Horizontalen abgeschossen und hat die
Anfangsgeschwindigkeit vo
= 1500m·s-1. Berechnen Sie die Schussweite und die Schusshöhe!
Welche maximale Schussweite kann das Geschoss mit dieser
Anfangsgeschwindigkeit erreichen? xW
= 198,63 km sh
= 28,67 km xW(max)
= 229,36 km sh(max)
= 57,34 km
home Stoff
zurück Übung
top
HA
- Einführung in die Dynamik
home Stoff
zurück Übung
top
HA
- Die physikalische Größe Kraft
home Stoff
zurück Übung
top
HA
- Kräfteaddition, Kräftezerlegung
home Stoff
zurück Übung
top
HA
- Die Newtonschen Axiome
home Stoff
zurück Übung
top
HA
- Spezielle Kräfte und Prinzip von d'Alambert
home Stoff
zurück Übung
top
Hausaufgaben
- Physik Klasse 11-II GK
nur für Klasse EA 11:
Lösungen für AB:
1/37
 |
a) xW
= 10,1 m |
 |
b) mit Wurfparabelgleichung: y
= -0,04905·x2 + 5
| x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| y |
4,95 |
4,8 |
4,56 |
4,2 |
3,77 |
3,23 |
2,6 |
1,86 |
1,03 |
0,095 |
|
 |
c) aus Wurfweitengleichung: xW = √((2yo·vox2)/g)
folgt bei yo und g = konstant: xW ~ √(vox2) also xW
~ vox |
1/38
 |
a) yo
= 19,62 m tF
= 2s |
 |
b) v =
28,02 m/s α =
-44,45° |
1/41
 |
in
Gleichung für Wurfparabel:
y
= -
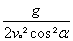 ·x² + tanα·x
+ yo für y eine Null einsetzen und die Gleichung nach vo
umstellen: vo = √((g·x2)/(2cos2α(tanα·x
+ yo))) vo
= 13,72 m/s
·x² + tanα·x
+ yo für y eine Null einsetzen und die Gleichung nach vo
umstellen: vo = √((g·x2)/(2cos2α(tanα·x
+ yo))) vo
= 13,72 m/s |
HA
- Arbeit und Energie
Aufgabe: Ein Pkw der Masse 800 kg
steigert seine Geschwindigkeit von 14 m/s auf 22 m/s in 4 s.
a) Welche Beschleunigungsarbeit
verrichtet der Motor an dem PKW?
Hinweis: Ermitteln Sie zunächst die
Beschleunigung und den dabei zurückgelegten Weg (Achtung: PKW hat eine
Anfangsgeschwindigkeit!) und benutzen Sie dann die Gleichung: WB
= m·a·s für die Berechnung der Beschleu- nigungsarbeit. a
=
∆v/∆t
= (8 m/s)/4s = 2 m/s2 s
= ½·a·t2 + vo·t
= 72m WB = m·a·s =
800kg·2m/s2·72m = 115,2kJ
b) Welche kinetische Energie besitzt der
PKW am Ende der Beschleunigungsphase gegenüber einem ruhenden Körper?
Ekin = WB = ½·m·v2 = ½·800kg·(22m/s)2
= 193,6 kJ
c) Welche kinetische Energie besitzt der
PKW am Ende der Beschleunigungsphase gegenüber einem mit 14m/s gleichförmig
weiterfahrenden LKW?
Ekin
= WB = 115,2 kJ
home Stoff
zurück Übung
top
HA
- Energieerhaltungssatz
1. Beim Curling verlässt ein Stein der Masse 5,3 kg
die Hand des Spielers mit einer Geschwindigkeit von 7,5m/s. Wie weit rutscht
dieser Stein, wenn von einer Reibungszahl von 0,065 für die Stoffkombination
Granit/Stein ausgegangen werden muss?
WR
= ∆Ekin
μ·m·g·s
= 0,5·m·v2 s = 44,1 m
2. Wie groß ist die Beschleunigungsarbeit die verrichtet
werden muss, um einen PKW der Gesamtmasse von 1,0t:
 | aus dem Stand auf 50
km/h
WB=
Ekin1-
Ekin0=
0,5·m·v2 - 0 = 96,45 kJ
|
 | von 50 km/h auf 100 km/h zu beschleunigen?
WB=
Ekin2
- Ekin1
=
0,5·m·v22 - 0,5·m·v12
= 289,35 kJ |
3. Ein Fadenpendel der Länge 1,0 m wird zunächst um
90° und später um 30° ausgelenkt. Berechnen Sie die maximale Geschwindigkeit
des Pendelkörpers beim Durchgang durch die Gleichgewichtslage (Ruhelage) für
beide Fälle?
EpotA + EkinA = EpotE
+ EkinE
nur Lageenergie im
Umkehrpunkt (Körper in Ruhe)
EpotA = EkinE
nur
Bewegungsenergie in Gleichgewichtslage
(auf Höhe h = 0)
m·g·h = 0,5·m·v2
bei 90°
Auslenkung: m·g·l = 0,5·m·v2
bei 30° Auslenkung:
m·g·l·(1-cosα)
= 0,5·m·v2
v = 4,43 m/s
v = 1,62 m/s
4. Ein Fahrzeug mit 40 km/h erzeugt bei
blockierten Bremsen eine Bremsspur von 10 m Länge. Wie lang ist seine Bremsspur
bei 160 km/h? Hängt die Länge der Bremsspur von der Masse des PKW ab?
WR = ∆Ekin
μ·m·g·s
= 0,5·m·v2 s = v2/(2·μ·g)
s ~ v2 ( μ = konst.) aus v2
= 4·v1 folgt s2 = 16·s1 = 160 m
7. Eine Straße fällt an einem Abhang um 15 m ab. Ein
Fahrradfahrer nähert sich dieser Stelle mit vo = 36 km/h.
Welche Geschwindigkeit hat er am Ende des Abhangs, wenn er nicht bremst und nur
so in die Pedale tritt, dass die Reibung aufgehoben wird?
Hinweis: Fertigen Sie eine Skizze des Sachverhaltes an, legen
Sie das Nullniveau der Höhe fest und überlegen Sie, an welcher Stelle der
Bewegung welche Energieformen vorliegen!
m·g·h + 0,5·m·v12
= 0,5·m·v22 v2
= √(2·g·h
+ v12) = 19,86 m/s
home Stoff
zurück Übung
top
HA
- Federspannarbeit
8. In einem Luftgewehr befindet sich eine Feder
(Federkonstante 100 N/m), welche im eingebauten Zustand bereits um 10 cm
vorgespannt ist. Beim Laden des Gewehrs wird diese Feder um weitere 7,5 cm
verformt. Mit welcher Geschwindigkeit verlässt eine Kugel der Masse 0,5 g den
Lauf dieser Waffe? Wie hoch könnte man mit dieser Waffe schießen?
Hinweis: Beachten Sie die Parallelen zu Aufgabe 2b!
EpotV1 = EpotV2 + Ekin
0,5·D·s12 = 0,5·D·s22 +
0,5·m·v2
v = √(D·s12
- D·s22)/m
= 64,2 m/s
Ekin
= EpotL 0,5·m·v2
= m·g·h h = v2/(2g)
= 210,24 m
home Stoff
zurück Übung
top
HA
- mechanische Leistung
home Stoff
zurück Übung
top
HA
- Impuls und Kraftstoß
2. Beim Schießen mit einem Kleinkalibergewehr erfährt man
einen merklichen Rückstoß. Berechnen Sie die Rückstoßgeschwindigkeit des
0,81 kg schweren Gewehrs, wenn das 6,1 g schwere Geschoss das Gewehr mit einer
Geschwindigkeit von 315 m/s verlässt und 30% des Rückstoßimpulses für das
Nachladen der nächsten Kugel genutzt wird! 0
= p1 + p2 0 = m1·v1
+ 0,7·m2·v2 v2 = 1,66 m/s
home Stoff
zurück Übung
top
HA
- elastischer Stoß
5. Eine Kugel der Masse 2 kg stößt mit einer
Geschwindigkeit von 10 m/s gerade und zentral auf eine ruhende Kugel der
Masse 3 kg.
Berechnen Sie die Geschwindigkeit beider Kugeln
- nach einem elastischen
Stoß
u1 = -2 m/s
u2 = 8 m/s
- nach einem unelastischen Stoß u = 4
m/s
7. Ein Wasserstoffmolekül stößt elastisch mit 200 km/h
gerade und zentral auf ein Sauerstoffmolekül, dass sich vor dem Stoß mit 110
km/h in entgegengesetzter Richtung auf das Wasserstoffmolekül zu bewegt.
Berechnen Sie die Geschwindigkeit beider Moleküle nach dem Stoß und
vergleichen Sie die Bewegungsrichtungen beider Moleküle vor und nach
dem Stoß!
home Stoff
zurück Übung
top
HA
- unelastischer Stoß
4. Ein Güterwagen mit der Masse 3 t rollt mit der
Geschwindigkeit von 5 m/s unter eine Ladevorrichtung. Dort wird er während
der Durchfahrt mit 10 t abgekippter Braunkohle beladen. Mit welcher
Geschwindigkeit verlässt der Wagen die Ladevorrichtung?
u = (3t·5m/s +
10t·0m/s)/13t
= 1,154 m/s
home Stoff
zurück Übung
top
HA
- gleichförmige Kreisbewegung
-
Ein
Hammerwerfer wirft sein Sportgerät 88 m weit. Wie groß ist die notwendige
Haltekraft durch den Sportler unmittelbar vor dem Abwurf, wenn der Radius
der Kreisbahn 1,8 m beträgt und der Hammer die Masse 7,25 kg besitzt? (Hinweis:
Wiederholen Sie die Gesetze des schrägen Wurfes, gehen Sie vom optima- len
Abwurfwinkel und von der
Abwurfhöhe Null aus!)
aus sw
= vo2/g
folgt
vo=29,4 m/s und F =
3,477 kN
home Stoff
zurück Übung
top
HA
- Drehbewegung - gleichförmige und gleichmäßig beschleunigte Rotation
- Die Spitze des
Minutenzeigers einer Turmuhr hat die Geschwindigkeit
v = 1,5 mm/s. Wie lang ist der Zeiger?
ω
= 0,001745 s-1 r =
0,86 m
home Stoff
zurück Übung
top
HA
- Dynamik der Rotation
- Welche Rotationsenergie
Erot besitzt
ein scheibenförmiges Messer mit der Masse
m=12 kg und dem Durchmesser von d=0,60 m eines
Folienschneideautomaten bei einer Drehzahl
n=78 min-1?
Erot=18,044
J
- Aus welcher Höhe h muss
ein Artist mindestens starten, damit er die abgebildete „Todesschleife“
sicher durchfährt? (Reibungswiderstände
und Eigenrotation des Fahrzeuges seien vernachlässigbar)
h
= ½·r = 1,5 m
Komplexe Übung:
Eine um 38,5° ausgelenkte Abrissbirne
mit der Masse 520 kg
und einer Seillänge von 6,80
m stößt mit der Geschwindigkeit
5,39 m·s-1 auf
einen Stein mit der Masse 18,4
kg. Der Stein liegt lose auf einer 6,85
m hohen Mauer lotrecht unter der
Aufhängung der Abrissbirne. Der Stoß darf als elastisch, gerade und zentral
aufgefasst werden. Auch die Reibung darf vernachlässigt werden.
-
Erläutern
Sie die Gültigkeit von Erhaltungssätzen beim zentralen elastischen Stoß!
Beim zentralen elasti-
schen Stoß gelten sowohl der Energieerhaltungssatz der Mechanik als
auch der Impulserhaltungssatz.
-
Berechnen Sie die Geschwindigkeiten
von Abrissbirne und Stein unmittelbar nach dem Stoß!
Epot
=
Ekin
m·g·l·(1 – cosα)
= ½·m·v²
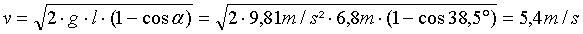
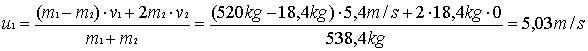
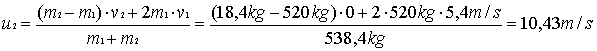
-
Berechnen Sie den größten
Auslenkwinkel, den die Abrissbirne nach dem Stoß erreichen kann!
Ekin
= Epot
½·m·u1² = m·g·l·(1 – cosα)
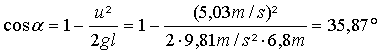
-
In welcher Entfernung von der Mauer
und nach welcher Flugdauer trifft der Stein am waagerechten Erdboden auf?
y
= ½·g·t²
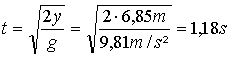 x
= u2
· t
=
10,43m/s
·1,18s
=
12,326m
x
= u2
· t
=
10,43m/s
·1,18s
=
12,326m
-
Berechnen Sie den Winkel zwischen der
Bahn des Steines und dem Erdboden beim Auftreffen!
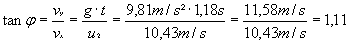 φ
= 47,98°
φ
= 47,98°
Übungsaufgabe : Energie und Impuls
52. Das
Geschoss (m1 = 10g) einer Pistole dringt gerade, zentral in einem
Holzklotz der Masse m2 = 600g ein, der auf einer horizontalen
Tischplatte liegt und dadurch 5,5m weit fortrutscht (Reibungszahl 0,4).
Berechnen Sie die Geschossgeschwindigkeit!
aus 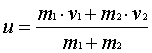 folgt
folgt
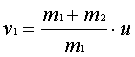 außerdem folgt aus
Ekin = WR
also ½·m·u2 =
μ·m·g·s
außerdem folgt aus
Ekin = WR
also ½·m·u2 =
μ·m·g·s
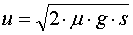 damit insgesamt:
damit insgesamt:
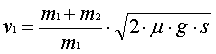 und damit v1
=
400,77 m/s
und damit v1
=
400,77 m/s
home Stoff
zurück Übung
top
Hausaufgaben
- Physik Klasse 12-I GK
HA
- Keplersche Gesetze
LB.S.171 /81
Die Entfernung Erde-Mars beträgt 78,4 Millionen Kilometer,
die Umlaufzeit des Mars um die Sonne 1,88 Jahre. Berechnen Sie aus diesen Werten
die Entfernung Erde-Sonne, also den Wert für die astronomische
Einheit! rSE = 149,832·106
km = 1AE (Tipp: Potenzgesetze)
Aufgabe:
Kometen sind riesigen, schmutzigen Schneebällen vergleichbare Körper von
einigen Kilometern Durchmesser. Sie umlaufen die Sonne auf langgestreckten
Ellipsenbahnen. Erst in Sonnennähe entsteht in günstigen Fällen ein Schweif,
der eine Länge von über 1 AE erreichen kann.
- Wie entsteht ein Schweif? Warum verliert der Komet an Materie?
- Seit mehr als 2000Jahren wird der immer in gleichen Abständen
wiederkehrende halleysche Komet beo- bachtet. Der letzte Periheldurchgang
fand 1986 statt, der nächste wird für das Jahr 2062 erwartet. Wie lang ist
die große Halbachse seiner Bahnellipse? ah
= 2,69·1012 m = 2,68·109 km rund 18 AE
(3.Gesetz)
- Im Perihel seiner Bahn ist Halley 90 Millionen Kilometer von der Sonne
entfernt. Wie weit ist er im Aphel von der Sonne entfernt? sa
= 5,3·1012 m = 5,3·109 km rund 35,4 AE
(Skizze)
home Stoff
zurück Übung
top
HA
- Gravitationsgesetz
AB Nr.1b,c
Berechnen Sie die Gravitationskraft zwischen:
- Erde und Mond! F = 1,99·1020N
- zwei Menschen mit 60kg bzw. 70 kg Masse und einem Abstand von 1
m! F = 2,8·10-7N
AB Nr.2b,c
| Gewichtskraft: FG = m · g |
3.
Keplersches Gesetz:
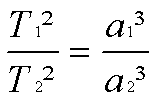 |
 | es wird der Zusammenhang zwischen
Gewichtskraft, Masse und der Fallbeschleunigung hergestellt |
 | gilt nur im annähernd homogenen
Gravitationsfeld in unmittelbarer Planetenoberflächennähe |
 | FG
~ m , wenn g = konstant
(an
einer bestimmten Stelle auf der Erde gilt: ein doppelt so schwerer
Körper hat auch eine doppelt so große Gewichtskraft) |
 | FG
~ g , wenn m = konstant
(ein
Körper hat auf einem hohen Berg eine kleine Gewichtskraft, weil da
die Fallbeschleunigung geringer ist) |
 | m ~
1/g , wenn
FG = konstant
(soll
ein Körper auf einem Himmelskörper mit kleiner Fallbeschleunigung
(z.B. Mond) die gleiche Gewichtskraft wie auf der Erde haben,
so muss er durch Zusatzmassen eine dementsprechend höhere Masse
bekommen) |
|
 | es wird der Zusammenhang zwischen den
Umlaufzeiten von Planeten und den großen Halbachsen ihrer
Umlaufbahnen hergestellt |
 | galt zunächst nur für unser Sonnensystem |
 | T2 ~
a3
(Uranus
hat eine höhere Umlaufzeit um die Sonne als Jupiter, weil er weiter
von der Sonne entfernt ist) |
|
AB Nr.3b,c
Wie groß ist die Gewichtskraft eines Körpers auf dem:
- Mars? FG(Mars) ≈ 2/5 · FG(Erde)
- Neptun? FG(Neptun)
≈ 17/16 · FG(Erde)
AB Nr.5
Zwischen der Erde und dem Mond gibt es eine Stelle, an der sich die
Gravitationskräfte von Erde und Mond auf einen dort befindlichen künstlichen
Himmelskörper gerade gegenseitig aufheben, man also ein Raumschiff parken
könnte. Berechnen Sie die Entfernungen dieses Punktes vom Erdmittelpunkt!
Ansatz: FEK = FMK
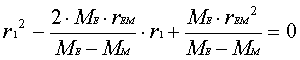 r12
- 389191554,3·r1 + 1,496·1017
= 0
r12
- 389191554,3·r1 + 1,496·1017
= 0
Entfernung
von der Erde :
(r11
= 431925 km) r12 = 345648 km
r11
entfällt, weil "hinterm" Mond und Gravitationskräfte heben sich
nicht auf , weil in die gleiche Richtung zeigend
home Stoff
zurück Übung
top
HA
- Schlussfolgerungen aus dem Gravitationsgesetz
AB Nr.4e,f
Leiten Sie die Gleichung zur Berechnung:
- der 1.kosmische Geschwindigkeit her, die man benötigt, um (auf
Meeresspiegelhöhe) um die Erde zu fliegen ohne auf die Erde zu fallen
v = 7,9 km/s
- der Bahngeschwindigkeit eines Satelliten in 200 km Höhe über der
Erdoberfläche her! Tipp: Ansatz: Fr Sat=
FGravitation Sat-Erde
- Bahngeschwindigkeit eines geostationären Satelliten
her!
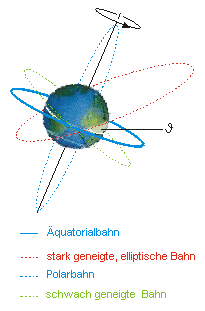
 |
soll
ein Satellit immer den gleichen Bereich der Erdober- fläche
beobachten, so muss er sich auf einem Kreis um den Erdmittelpunkt
bewegen (Großkreis) und die gleiche Winkelgeschwindigkeit (bzw.
Umlaufzeit) besitzen wie die Erdrotation
|
 |
dies
ist aufgrund der Gravita- tion zwischen Satellit und Erde nur in einer
gewissen Höhe über der Erdoberfläche möglich
|
 |
vom
Beobachtungsgebiet hängt der Neigungswinkel der Satelli- tenbahn zur
Äquatorialebene ab und davon wiederum der energetisch günstigste
Abflugort |
|
 |
F =
FZ
γ
·
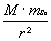 = mSa·
= mSa·
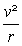 v
= ω·r
v
= ω·r
γ
·
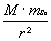 = mSa·ω²·r
ω=2Π·f=2Π/T
= mSa·ω²·r
ω=2Π·f=2Π/T
γ
·
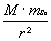 = mSa·
= mSa·
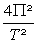 ·r /: mSa ·(r²·T²)
·r /: mSa ·(r²·T²)
γ
· M · T²
= 4Π² · r³
/ : (4Π²) /
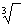
r
=
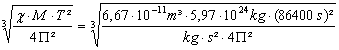
rE
+ h
= 42226,91
km
h = 42226,91 km - 6371 km
= 35855,91 km
h
≈ 36
000 km |
home Stoff
zurück Übung
top
HA
- Gravitationsfelder
83b) F(r)
=
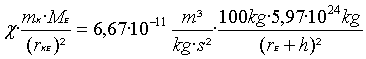
F(h)
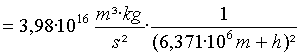
c)
aus F ~
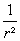 folgt:
wenn r2 = √2·r1
dann F2 = ½·F1
folgt:
wenn r2 = √2·r1
dann F2 = ½·F1
wenn r1= 6371 km muss also r2 =
9009,955 km sein und
wegen h = r2 – rE folgt h ≈ 2639 km
d)
FG (Garmisch) = 980,324 kg
FG (Zugspitze) = 979,635 kg
Verlust: 0,07%
85a)
Fr = FG
mA·ω²·(rE+h)
=
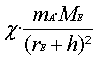 mA·
mA·
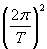 ·(rE+h) =
·(rE+h) =
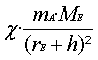
T = 2π·
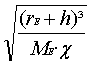
c) Fr = FG
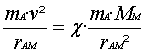
v =
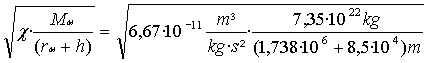 = 1640 m/s
= 1640 m/s
87a)
gMa =
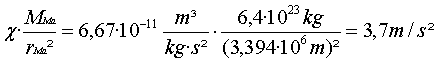
b,c)
v =
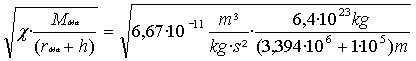 =
3495,4 m/s
=
3495,4 m/s
d,e)
F=gMa·mL=3,7m/s²·14000kg=51,8 kN
FS =FG+Fa= (24,05+45,5) kN = 69,55 kN
home Stoff
zurück Übung
top
HA
- Coulombsches Gesetz
Aufgabe: Welche elektrische Abstoßungskraft
üben zwei Protonen im Atomkern (nehmen Sie den
Atomkernradius mit ca. r = 5·10-15 an) aufeinander aus?
Warum zerfällt dann der Atomkern nicht?
Hinweis: Bedenken Sie ,dass jedes Proton als Ladung je eine
Elementarladung e trägt! Fel =
9,23N
Paetec LB. S. 371 Nr. 6
sinα =
Δx : l = 0,05m : 1,5 m α = 1,91°
tanα
= Fel
/ FG Fel = tanα·FG
Fel = tanα·m·g
= 1,636·10-4N
home Stoff
zurück Übung
top
HA - elektrisches
Feld
home Stoff
zurück Übung
top
HA - elektrische
Feldstärke
3. Ein Probekörper trägt eine Ladung von 10-10C.
In einem elektrischen Feld unterliegt er einer Kraftwirkung von 2·10-3N.
Wie groß ist die Feldstärke an dieser Stelle des Feldes? Geben Sie die
elektrische Feldstärke auch in V/m an!
E = F/q = (2·10-3N)/(1·10-10C)
= 2·107N/C = 20 000 000 V/m
4. An einem Plattenkondensator liegt eine Spannung von 5000
V an. Sein Plattenabstand beträgt 0,5 cm. Wie groß ist die elektrische
Feldstärke im Innern des Plattenkondensators? Welche Kraft wirkt im Innern des
Plat- tenkondensators auf einen Probekörper der Ladung -3·10-9C?
E = U/d = (5000V)/(0,005m) = 1·106V/m
E = F/q F = E·q = 1 000 000 N/C
·(-3·10-9C) = 0,003N = 3mN
5. Skizzieren Sie das Feldlinienbild eines Stabes, der an
seinen beiden Enden ungleichnamig geladen ist (Dipol)!
home Stoff
zurück Übung
top
HA - Spannung
und Potential
1. Eine Probeladung q = 3·10-9C befindet sich
2 cm von der positiven Platte entfernt im Feld eines Plattenkondensators mit 1
kV angelegter Spannung und einem Plattenabstand von 6 cm.
 | Berechnen Sie die elektrische Feldstärke im
Kondensatorfeld! E = U/s =
1000V/0,06m = 16667 V/m |
 | Berechnen Sie die Feldkraft , die auf die Probeladung
wirkt!
F = q·E = 3·10-9C·16667V/m = 5·10-5 N
|
 | Berechnen Sie das elektrische Potential an dieser Stelle
des Feldes! φ
= (U/s) ·x = 1000V/0,06m ·0,02m |
φ
= 333,3 V = ⅓·U,
weil x = ⅓·s
2.
Eine metallische Kugel mit r = 2,5 cm trage eine Ladung von 9·10-12C.
 | Berechnen
Sie die Feldstärke im el. Radialfeld der Kugel in den Punkte P1
und P2, welche 4,6 cm und 10 cm vom Kugelmittelpunkt entfernt
sind!
E1 = Q/(4πεo·r12)
= 38,2 V/m E2 = 8,1 V/m |
 | Bestimmen
Sie die Spannung zwischen den Punkte P1 und P2!
U12 = Q/(4πεo)·(1/x1 -
1/x2) = 0,95 V |
 | Welche
Kraft wirkt in den Punkte P1 und P2 auf eine positive
Probeladung q = 3·10-12C? F1
= 1,15·10-10N |
 | Welche
Arbeit muss verrichtet werden, um die Ladung q im Feld der Ladung Q
von P1 nach P2 zu
verschieben?
W12
= U12 · q = 0,95 V ·3·10-12C = 2,85·10-12J
= 17,8 MeV |
home Stoff
zurück Übung
top
HA - Kondensator
1. Gegeben sei ein Plattenkondensator mit kreisförmigen
Platten vom Durchmesser 16 cm und einem
Plattenabstand von s =5 mm.
- Welche Kapazität hat dieser Plattenkondensator?
C = 3,56·10-11 F = 35,6 pF
- Welche Ladung nimmt jede Platte auf, wenn eine
Spannung von 1 kV angelegt wird? Q = 3,56·10-8C
- Bestimmen Sie die elektrische Feldstärke im Innern
des Kondensators! E = 200000 V/m
- Berechnen Sie die Flächenladungsdichte!
σ
= 1,77·10-6 C/m2
- Mit welcher Kraft ziehen sich die Plattengegenseitig
an? F = E · Q = 7,12·10-3
N
Bestimmen Sie die Influenzladung auf einer
Metallplatte der Fläche A' = 20 cm2, die senkrecht zu den
Feldlinien in das Feld gehalten werden! q
= 3,54·10-9 C
Wie ändern sich die Werte für Kapazität,
aufgenommene Ladung und Feldstärke, wenn statt Luft ölgetränktes
Papier als Dielektrikum benutzt wird?
wegen C ~
εrel folgt: wenn εrel2
= 3·εrel1 so auch C2
= 3·C1
wegen
Q ~
C (aus C = Q/U ) folgt: wenn C2 = 3·C1
so
auch Q2 = 3·Q1
wegen
E ~
Q und E ~ 1/εrel
(aus E = Q/(εo·εrel·A)
) folgt: E2 = E1
weil beides sich
- Für Experimente wird ein luftgefüllter
Plattenkondensator aus zwei quadratischen Platten mit einer Kantenlänge von
20 cm, die einem Abstand von 2 cm zueinander aufweisen, aufgebaut. Er wird
mit einer Spannung von 400 V betrieben.
- Bestimmen Sie die Kapazität des Kondensators und
die Ladung, die er trägt! C=1,77·10-11F=17,7 pF
Q = 7,1·10-9 C
- Welche Feldstärke hat das elektrische Feld im
Innern des Kondensators und wie viel Energie ist in ihm gespeichert?
E = 20000 V/m Eel.Feld
= 1,42·10-6 J
- Nun wird der Kondensator von der Spannungsquelle
getrennt. Welche Werte nehmen die Kapazität, die elektrische
Feldstärke und die gespeicherte Energie an, wenn die Platten auf 3 cm
Abstand auseinander gezogen werden? C2
= ⅔·C1
= 11,8 pF E2 = E1=
20000
V/m Eel.Feld2 = 1,5·Eel.Feld1 = 2,1·10-6
J
- Der ursprüngliche Plattenabstand wird wieder
hergestellt und wieder eine Spannung von 400 V angelegt. Jetzt wird der
Kondensator in ein Ölbad eingebracht, so dass die Luft zwischen den
Platten vollständig durch das Öl verdrängt wird. Dabei wurde
nachgewiesen, dass von der Spannungsquelle eine zusätzliche Ladung von
Q = 9,9·10-9C zum Kondensator floss. Wie groß ist die
Dielektrizitätszahl εr
des verwendeten Öls? εrel
=
2,4
-
Drei Kondensatoren mit einer Kapazität
von 1μF,
2μF und 4μF stehen zur Verfügung.
-
Welche
maximale und welche minimale Kapazität kann man durch Zusammenschalten
aller drei Kondensatoren erreichen? Cmin
=
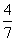 μF Cmax = 7 μF
μF Cmax = 7 μF
-
Lässt
sich eine Gesamtkapazität von
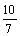 μF
durch Kombination aller drei Kondensatoren erreichen? Begründen Sie
Ihre Auswahl und Ihre Schaltung!
ja,
den 4μF und den 1μF parallel und dazu in Reihe den 2μF
Kondensator schalten
μF
durch Kombination aller drei Kondensatoren erreichen? Begründen Sie
Ihre Auswahl und Ihre Schaltung!
ja,
den 4μF und den 1μF parallel und dazu in Reihe den 2μF
Kondensator schalten
home Stoff
zurück Übung
top
HA - Millikan-Versuch
home Stoff
zurück Übung
top
HA - Bewegung
von Elektronen im homogenen elektrischen Feld
1. Ein Elektron tritt mit einer kinetischen Energie Ekino
= 2,5·10-18 J parallel zu den Feldlinien in ein homogenes
Kondensatorfeld ein.
- Welche Geschwindigkeit hat das Elektron vor dem
Einfliegen in das elektrische Feld? vo
= 2,344·106 m/s
- Welche Potentialdifferenz durchläuft das Elektron,
wenn es beim Verlassen des Feldes gerade die Geschwindigkeit Null
hat? U = 15,6 V
- Welche Potentialdifferenz durchläuft das Elektron,
wenn es beim Verlassen des Feldes nur noch die halbe Geschwindigkeit
besitzt? U = 11,7 V
2. Ein Elektron mit der Geschwindigkeit von 5·106
m·s-1 wird senkrecht zu den Feldlinien in das homogene Feld eines
Plattenkondensators geschossen. Der Kondensator hat eine Länge von l = 5
cm; der Plattenabstand d beträgt 2 cm.
- Berechnen Sie die Ablenkung des Elektronenstrahls auf einem 15 cm
entfernten Leuchtschirm, wenn die Ablenkspannung an den Kondensatorplatten
2,5 V beträgt! yD =
9,5064·10-2 m
- Wie groß müsste die Kondensatorspannung gewählt werden, damit das
Elektron den Kondensator gerade nicht mehr verlässt? Hängt diese
Spannung vom Eintrittspunkt des Elektrons in das Feld
ab? U = 31,6 V ;
ja, je höher das Elektron einfliegt, umso größer muss U sein
home Stoff
zurück Übung
top
HA - Magnetfeld
home Stoff
zurück Übung
top
HA - Magnetische
Flussdichte
home Stoff
zurück Übung
top
HA -
Magnetfeld einer Spule
Mit einer Zylinderspule (l = 20 cm; d = 5 cm)
soll eine magnetische Flussdichte von 1,5·10-2T erzeugt werden.
- Wie groß muss die Windungszahl bei einer Stromstärke
von 6A sein? N ≈
400
- Welche Spannung muss angelegt werden, wenn die Stärke
des Kupferdrahtes 0,5 mm beträgt (Spule einlagig gewickelt)?
U = 32,5V
home Stoff
zurück Übung
top
HA - Lorentzkraft
Die von einem elektrischen Feld beschleunigten Elektronen
treten senkrecht zu den Feldlinien in ein homogenes Magnetfeld der
Flussdichte B = 1,2 mT ein und
werden auf eine Kreisbahn mit
dem Radius r = 25 mm
gezwungen.
- Berechnen sie die Eintrittsgeschwindigkeit der
Elektronen! (Hinweis: entnehmen Sie die Werte
für Elektronenladung und -masse dem Tafelwerk) v
= (e·r·B)/me = 5,28·106 ms-1
- Wie groß muss die Beschleunigungsspannung für die
Elektronen im elektrischen Feld gewesen sein?
U = (me·v2)/(2·e) = 79,21
V
oder U = (e·r2·B2)/(2·me)
= 79,22 V
home Stoff
zurück Übung
top
HA - Anwendungen zur
Lorentzkraft
home Stoff
zurück Übung
top
HA - Analogie zwischen
den Feldern
home Stoff
zurück Übung
top
Hausaufgaben
- Physik Klasse 12-II GK
home
zurück top
HA - Elektromagnetische
Induktion
home Stoff
zurück Übung
top
HA - Der magnetische
Fluss
home Stoff
zurück Übung
top
HA - Induktionsgesetz,
Lenzsche Regel
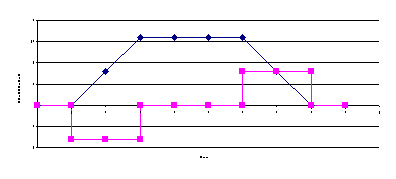
-
Ein
quadratischer Rahmen mit einer Seitenlänge von 8,0 cm aus Kupferdraht (5,0
cm² Querschnittsfläche) wird in 0,4 s gleichmäßig in ein homogenes
Magnetfeld der magnetischen Flussdichte 0,2 T senkrecht zu den Feldlinien
eingeschoben (siehe Skizze)
-
Berechnen
Sie die dabei induzierte Spannung!
Uind = (B·∆A)/∆t
= (B·∆a2)∆t
= (0,2T·(0,08m)2)/0,4s = 0,0032V
-
Wie
groß ist der daraufhin fließende Induktionsstrom?
I = U/R = (U·AØ)/(ρ·l)
= (0,0032V·500mm2)/(0,017Ωmm2m-1·0,32m)
= 294,1A
-
Welche
Kraft muss beim Einschieben am Rahmen angreifen?
FL
= I·l·B = 294,1A·0,08m·0,2T = 4,7N
-
Berechnen
Sie die beim Einschieben verrichtete Arbeit auf zwei verschiedene Arten! Emech = F·s = 4,7N·0,08m
= 0,376J Eel
= U·I·t = 0,0032V·294,1A·0,4s = 0,376J
-
Wie
ändert sich die Leistung beim Einschieben, wenn der Vorgang in der halben
Zeit abläuft?
wegen P = W/t = E/t also P
~
1/t (W=E=konstant) führt Halbierung der Einschubzeit zur Verdopplung
der Leistung
Paetec LB.S.375 Nr.36
- Φ
= A · B = N·Ao·B =
N·a2·B = 20 · (0,2m)2
· 0,02T Φ
= 0,016 Wb
Uind = -∆Φ/∆t =
-
0,016Wb/2s = -0,008V
|
|
AB Nr.4
-
Uind2
= -∆Φ/∆t = -∆(N2·Ao2·B)/∆t
= -N2·Ao2·∆B/∆t = -N2·Ao2·∆(μ·N1·I/l1)/∆t
= -N2·Ao2·μ·N1·∆I/(∆t·l1)
Uind2 = -2000 ·1,6·10-3 m2 · 1,256·10-6
VsA-1m-1 · 300 · (-2,5A) /(8·10-3s · 0,2m)
= 1,884 V
-
Uind2
= -∆Φ/∆t = -∆(N2·Ao2·B·cosφ)/∆t
= -N2·Ao2·cosφ·∆B/∆t = -N2·Ao2·μ·N1·cosφ·∆I/(∆t·l1)
= 0,942 V
home Stoff
zurück Übung
top
HA - Selbstinduktion,
Wirbelströme
B Nr.4
-
Uind1
= -∆Φ/∆t = - L · ∆I/∆t
= -(μ·N12·Ao1·∆I)/(l1·∆t)
Uind1 = - ( 1,256·10-6
VsA-1m-1 · 3002 · 1·10-2 m2 · (-2,5A)) /(0,2m · 8·10-3s)
= 1,766 V
-
Uind1
= 1,776 V , weil die
relative Lage beider Spulen keinen Einfluss auf die Selbstinduktion von
Spule 1 hat
home Stoff
zurück Übung
top
HA - Generator und
Dynamomaschinen
home Stoff
zurück Übung
top
HA - Transformator
-
Mit
einem Wechselstrom der Spannung von 220 V soll in 10 km Entfernung eine Glühlampe
mit einer Leistung von 100W betrieben werden. Berechnen Sie die
Verlustleistung, welche sich durch Wärmeverluste in den Zuleitungen
bemerkbar macht, wenn Aluminiumleitungen der Querschnittsfläche 2,3 mm²
verwendet werden, unter folgenden Voraussetzungen:
-
Die
Lampe wird durch die Zuleitungen direkt mit der Spannungsquelle verbunden. I=P/U=0,4545A R=ρ·(l/A)=243,5Ω
PV=U·I=R·I2=50,3W
-
Zwischen
der Lampe und der Spannungsquelle befinden sich zwei Transformatoren mit 95%
Wirkungs- grad, welche die Spannung in den Zuleitungen um den Faktor 10
herauf- bzw. herabtransformieren. I=P/U=95W/2200V=0,04318A
R=ρ·(l/A)=243,5Ω
PV=U·I=R·I2=0,454W für den
gesamten Übertragungsweg gilt damit: PV= 5W + 0,454W +
4,75W = 10,2W
-
Gegeben
sei ein Transformator mit:
Spule
1:
N = 2500,
l = 50 cm,
A = 450 cm²,
B = 1,2 T,
μrel
= 150
Spule
2:
N = 500,
A = 15 cm²,
-
Berechnen
Sie die fließende Stromstärke I, die Induktivität L und die gespeicherte
Energie in der Spule 1! I=(B·l)/(μo·μrel·N)=1,274A
L=106H
E=82,4J
-
Berechnen
Sie die Spannung U2 in der Sekundärspule, wenn an der Primärseite
220 V angelegt werden (unbelasteter Trafo!)!
U2
= 44V
-
Wird
der Sekundärstromkreis über einen 50Ω-Widerstand geschlossen, fließt
ein Sekundärstrom I2. Berechnen Sie diesen für den Fall eines
idealen, belasteten Transformator!
I2=6,235A
-
Um
welche Art des Transformators handelt es sich (Auf- oder Abwärtstrafo)?
Abwärtstransformator
-
Wird
nun ein Schalter in Stromkreis 1 geöffnet, bildet sich zwischen den
Kontakten ein Abrissfunken. Erklären Sie diese Erscheinung und berechnen
Sie die entsprechende Größe für den Fall, dass der Abschaltprozess 20 ms
dauert! Uind=-L·(∆I/∆t)=33kV
-
Bei
einem Transformator gilt:
N1
= 1000; N2 = 750;
U1 = 24 V; I1
= 4 mA; R2 = RL
= 5 kΩ
Berechnen
Sie die Stromstärke und Spannung sowie die elektrische Leistung im Sekundärstromkreis!
(benutzen Sie dabei keine Gleichungen, die nur für den unbelasteten
Transformator gelten!)
I2=(N1/N2)·I1=5,33mA
U2=RL·I2=26,66V P2=U2·I2=0,142W
home Stoff
zurück Übung
top
Hausaufgaben
- Physik Klasse 13-I GK
HA - Reflexion und
Brechung
Aufgabe: Der Einfallswinkel eines Lichtstrahls auf
eine ebene Grenzfläche beträgt 55°. Wie groß ist der Winkel γ
zwischen reflektiertem und gebrochenem Strahl, wenn die Brechzahl 1,5 beträgt?
(Skizze machen)
sinβ
= sinα
:
n = sin55° : 1,5 β
= 33,1° außerdem α'
=
α
=
55° γ =
180° - α'
-
β
= 180° - 55° - 33,1° = 91,9°
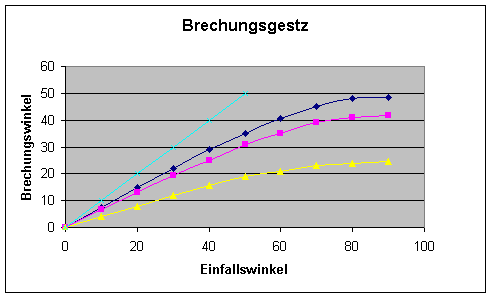
Aufgabe: Die Einfallswinkel eines Lichtstrahls
betragen an einer Grenzfläche Luft-Wasser 30°, 45°, 60° bzw. 75°. Wie
groß sind die Brechungswinkel?
sinβ
= sinα
:
n = sin30° : 1,33 β1
= 22,0° außerdem β2
= 32,0° β3
= 40,5° β4
= 46,4°
rotes
Paetec LB.S.432 Nr.8
 | Brechungswinkel nimmt mit steigendem
Einfallswinkel zu |
 | Zunahme (Anstieg) des Brechungswinkels nimmt
mit steigendem Einfallswinkel ab |
 | bei 90° Einfallswinkel geht die Kurve in eine
Waagerechte über |
 | dort ist der Grenzwin- kel der Totalreflexion
ablesbar |
 | αG (Wasser) =
48,6° |
 | αG (Glas) =
41,8° |
 | αG (Wasser) =
24,6° |
|
|
 | der gestrichelte
Verlauf (Gerade) ist nur möglich, wenn Einfallswinkel gleich
Brechungswinkel |
 | dies könnte bei einer Stoffkombination
auftreten, bei der beide Stoffe die gleiche Brechzahl besitzen, die
relative Brechzahl also 1 ist (z.B.: Zedernholzöl- Glas) |
|
home Stoff
zurück Übung
top
HA - Totalreflexion,
planparallele Platte
Aufgabe: Ein Lichtstrahl fällt unter einem
Winkel von 45° auf eine planparallele Platte der Dicke d = 5 cm aus leichtem
Kronglas. Berechnen Sie den Abstand zwischen den reflektierten Strahlen der 0.
und 1.Ordnung! Beurteilen Sie die Intensität der beiden Strahlen unter der
Bedingung, dass die zweite Grenzfläche zwischen Glas und Luft voll verspiegelt
ist und bei jeder unverspiegelten Grenzfläche 10% des einfallenden Lichtes reflektiert werden!
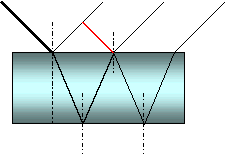
sinβ
=
(sinα
·
n1) : n2 =
(sin45°·1):1,51 β
=
27,9°
cosβ
=
AB :
AC AC = AB : cosβ
=
5cm : cos27,9°
= 5,66 cm (im Dreieck ABC)
AE2
= AC2+CE2-2·AC·CE·cos2β=2·AC2-2·AC2·cos2β=2·(5,66 cm)2-2·(5,66 cm)2·cos55,8°
(im Dreieck ACE)
AE= 5,30 cm
sinα'
= EF :
AE EF = AE · sinα'
= 5,30 cm ·sin45° = 3,74 cm (im Dreieck AEF)
1.Grenzschicht: 90% gebrochener Strahl ins Glas
10% reflektierter Strahl in
die Luft
2.Grenzschicht: 90% reflektierter Strahl ins Glas zurück
3.Grenzschicht: 9% reflektierter Strahl ins Glas zurück
81%
gebrochener Strahl in die Luft
4.Grenzschicht: 9% reflektierter Strahl ins Glas zurück
5.Grenzschicht: 0,9% reflektierter Strahl ins Glas zurück
8,1% gebrochener
Strahl in die Luft
Resumeé:
Sowohl die reflektierten Strahlen 0. und 1. Ordnung, als auch die reflektierten
Strahlen 1. und 2. Ordnung unterscheiden sich in ihrer Lichtintensität ganz
erheblich!
LB.S.433
Nr.12
Licht
trifft unter dem Einfallswinkel α
auf
eine planparallele Platte der Dicke d aus durchsichtigem Material.
Untersuchen Sie die Abhängigkeit des Parallelabstandes x zwischen dem
einfallenden und dem austretenden Lichtstrahl von:
- dem
Einfallswinkel α
- von
der Brechzahl n der Platte
- von
der Dicke der Platte
|
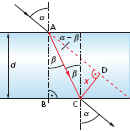
|
- wenn
d ↑ so
auch x ↑ (aus *)
- wenn α ↑ (und
damit auch β ↑,
aber nicht so schnell) so auch x ↑ (aus *)
- wenn
n ↑ so
auch x ↑ (aus **)
|
| sinβ
=
(sinα
·
n1) : n2 bei der Kombination Luft-Stoff gilt :
sinβ
=
sinα/n
AC = AB :
cosβ
γ
=
α -
β
CD = AC · sinγ
|
(*)
x
= CD = AC · sinγ
x=(AB/cosβ)·sin(
α-β)
x
=
d·(sin(α-β)/cosβ)
oder
siehe LB. S 389 |
(**)
x=CD=AC·sinγ=(AB/cosβ)·sin(α-β)
x=(d/cosβ)·(sinα·cosβ-cosα·sinβ)
x
= d · (
sinα
- cosα·tanβ
)
(mittels
Additionstheorem)
|
home Stoff
zurück Übung
top
HA - Abbildung mittels
Sammellinsen
Aufgabe: Konstruieren Sie das
Bild eines Gegenstandes bei Abbildung mit einer Sammellinse mit f = +30mm, wenn
der Gegenstand 2cm groß ist und in 1,5cm Entfernung von der Linse aufgestellt
wird!
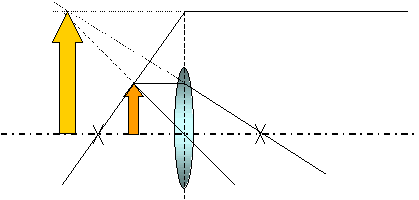
Durch Verlängerung der zunächst divergenten Strahlen auf die
Gegenstandsseite der Linse erhält man im dortigen Schnittpunkt von
Mittelpunkts-, Brennpunkts- und Parallelstrahl das virtuelle,
vergrößerte, aufrechte Bild des Ge- genstandes, so wie man es mit einer Lupe
beobachten kann (jede Sammellinse kann also als Lupe benutzt werden).
home Stoff
zurück Übung
top
HA - Abbildungsgleichung
für dünne Sammellinsen
AB "Übungsaufgaben: Strahlenoptik" Nr.8
| Gegenstandsweite
s in cm |
Brennweite f in cm |
| 10 |
20 |
30 |
40 |
50 |
| 10 |
0 |
-20 |
-15 |
-13,3 |
-12,5 |
| 20 |
20 |
0 |
-60 |
-40 |
-33,3 |
| 50 |
12,5 |
33,33 |
75 |
200 |
0 |
| 100 |
11,11 |
25 |
42,8 |
66,66 |
100 |
| 1000 |
10,1 |
20,4 |
30,9 |
41,6 |
52,6 |
AB "Übungsaufgaben: Strahlenoptik" Nr.9
Ein Gegenstand, der 10 cm groß ist und sich in 2 m Entfernung vor einer
Linse mit einer Brennweite von 250 mm befindet, soll mit Hilfe dieser Linse
scharf abgebildet werden. In welcher Entfernung von der Linse entsteht das
Bild? Wie groß ist es? s' = 28,6
cm y' = 1,4 cm
Aufgabe:
home Stoff
zurück Übung
top
HA - Abbildung mittels Spiegel und Hohlspiegel
Aufgabe:
home Stoff
zurück Übung
top
HA - optische Geräte
Aufgabe:
home Stoff
zurück Übung
top
HA - Abbildungs- und Sehfehler
Aufgabe:
home Stoff
zurück Übung
top
HA - Einführung in
die Wellenoptik
Aufgabe:
home Stoff
zurück Übung
top
HA - Kohärenz,
Beugung und Interferenz an Doppelspalt und Gitter
Aufgabe: Ein Doppelspalt wurde mit
monochromatischem (einfarbigem) Licht beleuchtet. Der Abstand der Maxima auf dem
2,4 m entfernten Schirm betrug s1= 3,5 mm. Um den Spaltabstand b zu ermitteln,
wurde der Doppelspalt mit einer in 20 cm Entfernung aufgestellten Linse auf dem
Schirm scharf abgebildet. Der Abstand der Spaltbilder betrug 5,1 mm. Berechnen
Sie die Wellenlänge des verwendeten Lichtes und benennen Sie seine Farbe!
(Hinweis: Das geht tatsächlich, ohne
die Brennweite der Linse zu kennen!)
home Stoff
zurück Übung
top
HA - Interferenz an
dünnen bzw. keilförmigen Schichten
Aufgabe:
home Stoff
zurück Übung
top
HA - Polarisation
und Spannungsdoppelbrechung
Aufgabe:
home Stoff
zurück Übung
top
HA - Einführung in
die Quantenoptik
Aufgabe:
home Stoff
zurück Übung
top
HA - Der äußere
lichtelektrische Effekt (Photoeffekt)
Aufgabe:
home Stoff
zurück Übung
top
HA - Das
Bohr-Sommerfeldsche Atommodell
Aufgabe:
home Stoff
zurück Übung
top
Hausaufgaben
- Physik Klasse 13-II GK
HA - Der
Franck-Hertz-Versuch
Aufgabe:
home Stoff
zurück Übung
top
HA - Spektralanalyse
Aufgabe:
home Stoff
zurück Übung
top
HA - Laser
Aufgabe:
home Stoff
zurück Übung
top
HA - Röntgenstrahlung
Aufgabe:
home Stoff
zurück Übung
top
HA - Eigenschaften von
Mikroobjekten
Aufgabe:
home Stoff
zurück Übung
top
HA - Grundkenntnisse
über Atomkerne
Aufgabe:
home Stoff
zurück Übung
top
HA - Eigenschaften
radioaktiver Strahlung
Aufgabe:
home Stoff
zurück Übung
top
HA - Nachweisgeräte
für radioaktive Strahlung
Aufgabe: Beschreiben Sie den Aufbau eines
Geiger-Müller-Zählrohrs und erklären Sie die seine Wirkungsweise !
home Stoff
zurück Übung
top
HA - Natürliche
Radioaktivität
Aufgabe:
home Stoff
zurück Übung
top
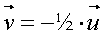





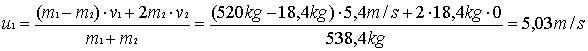
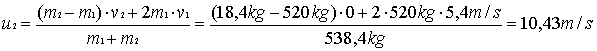
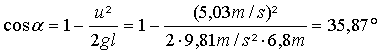
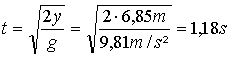
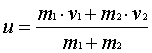
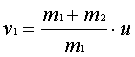
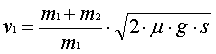 und damit
und damit