nach Termen mit gemeinsamer Variablenkonstellation ordnen
zusammenfassen durch Ausklammern der gemeinsamen Variablenkonstellation
Tägliche Übungen - Mathematik Klasse 11-I GK
1.) Zusammenfassen von Termen
|
nach Termen mit gemeinsamer Variablenkonstellation ordnen | |
|
zusammenfassen durch Ausklammern der gemeinsamen Variablenkonstellation |
|
Koeffizienten und Variablen gesondert multiplizieren | |
|
bei Variablen gegebenenfalls Potenzschreibweise (und –gesetze) nutzen |
|
erst
Multiplikationsterme vereinfachen, dann zusammenfassen |
|
gleiche Vorzeichen:
Beträge addieren, Vorzeichen bleibt | |
|
ungleiche Vorzeichen: Beträge subtrahieren, Vorzeichen von Zahl mit
größerem Betrag | |
|
Additionszeichen zwischen Termen kann wegfallen |
|
Gesamtvorzeichen
Minus bei ungerader Anzahl von Minuszeichen | |
|
Punktrechnung
(RO zweiter Stufe) geht vor Strichrechnung (RO erster Stufe) |
3.) Rechnen mit Klammern
|
Plusklammer:
Pluszeichen und Klammer fallen weg; alle Terme in der Klammer
behalten ihr
Vorzeichen bei | |
|
Minusklammer:
Minuszeichen und Klammer fallen weg; von allen Terme in der Klammer ist das
Entgegen- gesetzte zu bilden | |
Mehrfachklammern:
schrittweise von innen nach außen auflösen |
|
jeder Summand in der Klammer ist mit dem (vorzeichenbehafteten) Faktor außerhalb der Klammer zu multiplizieren |
5·(
3x – 2 )
= 15x – 10
7·(
4s – 3t ) - 8·( 2s + 5t )
= 28s – 21t – 16s
– 40t
= 12s – 61t
–4t·(
2s – 3 ) + 2s·( 4t – 3 )
= -8st + 12t + 8st –
6s
= 12t – 6s
(
5k – 4 )·5 - 2·( 8k – 10 )
= 25k – 20 – 16k +
20
= 9k
2x·( 2 – 2x + 5y )
– 2y·( 5x – 2 )
= 4x – 4x² + 10xy –
10xy + 4y
= -4x² + 4x + 4y
–3(4a–3b–3b²+2a²)–4(-3a–1,5a²
= -12a +9b +9b² -6a²
+12a +6a²
= 9b² + 9b
4x(
x – y) –[ 3x(
x +y) –2x(
x –y)]
= 4x² - 4xy – [
3x² + 3xy – 2x² + 2xy]
= 4x² - 4xy – 3x² -
3xy + 2x² - 2xy
=
3x² - 9xy
5(-2a+b)–2[(3a–5b)·4+(12–9a)·a]=
-10a + 5b – 2[ 12a – 20b + 12a – 9a²]
=-10a
+5b – 4a +40b –24a +18a²
= 18a² - 58a + 45b
4[ 4s(t–s)
– (s+4t)·3]
– 7s(s+8) = 4[
4st – 4s² - 3s – 12t ] – 7s² - 56s
= 16st –16s² -12s
–48t –7s² -56s
= -23s² - 68s + 16st – 48t
10.
(-2)[(-3t)(2a
– b) – (-4a)(10
– 2t)]
– (-6)(3a + 7t) = (-2)[-6at + 3bt + 40a –
8at] + 18a +42t
= 12at – 6bt – 80a + 16at + 18a + 42t
=
-62a + 28at – 6bt + 42t
|
jeder Summand der einen Klammer ist mit jedem Summanden der anderen Klammer zu multiplizieren | |
|
beachten Sie die Struktur der Terme (Summe, Differenz, Produkt, Quotient, Potenz) |
(
7t + 8e )( x + 1 )
=
7tx + 7t + 8ex + 8e
(
5t² - 8t )( 2t³ + 4 )
=
10t5 – 16t4 + 20t² - 32t
(
4x² + 2,5y )( -x – 2y )
= -4x³ - 8x²y – 2,5xy – 5y²
(2x–3y–2)(4–2x+2y)=8x
–4x² +4xy –12y +6xy –6y² -8 +4x –4 = -4x² + 12x + 10xy – 16y – 6y² - 8y
(
x – 2)( -3x – 5 – y) = -3x² -5x –xy +6x +10 +2y
= -3x² + x – xy + 2y + 10
(2x+y)(x–y)–[(x+3)(2x–4y)+3(4y–2x)]=2x²-2xy+xy–y²-[2x²-4xy+6x-12y+12y–6x]
= + 3xy – y²
(
a + b )( 2a – 1 )·b
= (2a² - a + 2ab – b)·b
= 2a²b – ab +
2ab² - b²
(x
– 1)(x² + 2x – 1) – (x² - 2x + 1)(x + 2) = x³ +2x² -x –x² -2x +1 = x³ + x² - 3x + 1
a(3a
– b + 2ab – 1) – (a – b)(3a – b) = 3a² -ab +2a²b –a – [3a²
-3ab –ab +b²]
= 2a2b + 3ab –
a – b²
(-3x)(2x+3y)-(2x–3y)(3+4x–2y)=-6x²-9xy–[6x+8x²-4xy–9y–12xy+6y²]= -14x² - 6x + 7xy + 9y – 6y
3.4) Ausklammern (Faktorisieren)
|
gemeinsame Faktoren aller Summanden vor die neugebildete Klammer | |
|
die Restglieder in der Klammer erhält man durch Division der Ausgangssummanden mit dem auszuklam- mernden Term |
4xy + 2x – 6xy = 2·2·x·y
+ 2·x – 2·3·x·y
= 2x · ( 2y
+ 1 – 3y ) =
2x·(-y +1)
![]() a +
a +
![]() b -
b -
![]() c
=
c
=
![]() · 2a +
· 2a +
![]() · 5b -
· 5b -
![]() · c
=
· c
=
![]() · (2a + 5b – c)
· (2a + 5b – c)
42abc² - 30ab²c – 28a²bc = 2·3·7·a·b·c·c
– 2·3·5·a·b·b·c
– 2·2·7·a·a·b·c
a³ - 2a² + 4a
= a·a·a
– 2·a·a + 2·2·a
= a · ( a² - 2a + 4 )
–a – b
= -1·a
– 1·b
=
-1 · ( a + b )
a(
5x – 2y ) – b( 5x – 2y )
= ( a – b ) · ( 5x –
2y )
x( 3a – b ) + y(-3a
+ b ) + 3az – bz
= x·(
3a – b ) - y·( 3a – b ) + z·(
3a – b )
3at –
5bt + 3as –
5bs = 3a ·(
t + s ) – 5b ·( t + s )
= ( 3a – 5b ) · ( t + s )
3bx–7ax+6b²-14ab–12ab+28a²=3·b·x–7·a·x+2·3·b·b–2·7·a·b-2·2·3·a·b+2·2·7·a·a=(3b-7a)·(x+2b-4a)
oder =
3b
·
(x
+
2b)
+a ·
(-7x
-
26b
+
28a)
sx²y–tx²y+3ps–3pt–4as+4at=s·x·x·y–t·x·x·y+3·p·s–3·p·t–4·a·s+4·a·t
|
benutzen
Sie die Formeln aus dem Tafelwerk
| |
|
verwandeln
Sie Binome in Summen bzw.
Summen zurück in Binome |
( s + t )² = s² + 2st + t²
(
12s + 4t )²
= 144s² +
96st + 16t²
( 5x + 6y
)²
= 25x² +
60xy + 36y²
(
9a + 6b )²
= 81a² +
108ab + 36b²
4s²
+ 12st + 9t²
= (2s + 3t)²
9x² + 4y²
+ 12xy
= (3x + 2y)²
t² + 2t
+ 1
= (t + 1)²
400n² +
9m² + 120mn
= (20n + 3m)²
( 1,2x +
5y )²
= 1,44x² + 12xy + 25y²
( s
– t )²
= s²
- 2st + t²
( 8n – 0,5m )²
= 64n² - 8mn + 0,25m²
k² - 24kl + 144l²
= (k – 12l)²
16s²
+ 25t² - 40st
= (4s - 5t)²
x²
-x +
0,25
= (x -
0,5
)²
x²
- 2x + 1
= (x – 1)²
25d²
+ 36c² - 60cd
= (5d – 6c)²
9x² + 64y² - 24xy = kein vollständiges Quadrat (-24xy ist kein doppeltes Produkt!)
x4
+ 100 – 20x²
= (x² - 10)²
4x² +
0,25·
y² - xy
= (2x -
0,5
y)²
(
2s + 5t )( 2s – 5t )
= 4s²
- 25t²
( x
+ 12s )( x – 12s )
= x²
- 144s2
( 16x –
11y )( 16x + 11y )
= 256x² - 121y²
9y² - 25
= (3y + 5)·(3y – 5)
169 –
144x²
= (13 + 12x) ·(13 – 12x)
196a² -
225b²
= (14a + 15b)·(14a
– 15b)
256p² -
16pq +
0,25
q²
= (16p -
0,5
q)²
![]() x² -
x² -
![]() y² = (
y² = (
![]() x +
x +
![]() y)· (
y)· (
![]() x -
x -
![]() y)
y)
36a² -
4ab +
b²
= (6a – 2b)²
![]() + 2x + 100x²
= (
+ 2x + 100x²
= (
![]() + 10x)²
+ 10x)²
(
![]() x² - 6x )² =
x² - 6x )² =
![]() x4 – x³ + 36x²
x4 – x³ + 36x²
x4
– y4
= (x²
+ y²)·(x² - y²)
4x4
– 25x²
= (2x² + 5x)·(2x² - 5x)
![]() a² -
a² -
![]() b²
= (
b²
= (
![]() a +
a +
![]() b)· (
b)· (
![]() a +
a +
![]() b)
b)
6.) Bruchterme
6.1)
Grundmenge und Definitionsbereich
Aufgabe:
Bestimmen Sie den Definitionsbereich folgender Bruchterme bzgl. des Grundbereichs der rationalen
Zahlen!
|
beachten Sie: ein Bruch ist nicht definiert , wenn der Nenner Null und der Zähler ungleich Null ist | |
|
sollten
beide Terme für eine Zahl Null werden, kann der Bruch gekürzt werden |
6.2)
Erweitern von Bruchtermen
Aufgabe: Erweitern Sie den Bruchterm mit dem angegebenen Erweiterungsfaktor!
|
beachten Sie: Erweitern eines Bruches bedeutet , Zähler und Nenner mit dem gleichen Term multiplizieren | |
|
nutzen
Sie danach ihre Fertigkeiten beim Multiplizieren von Summen |
Aufgabe: Erweitern Sie den Bruchterm so dass der angegebene Nenner entsteht!
| ermitteln Sie zunächst den Erweiterungsterm durch Division des neuen Nenners durch den alten Nenner | |
| erweitern Sie danach den Bruch wie in den vorhergehenden Aufgaben |
Aufgabe: Machen Sie die jeweils gegebenen Bruchterme gleichnamig!
|
ermitteln Sie zunächst den Hauptnenner beider Brüche als kleinstes gemeinsames Vielfache (kgV) beider Nenner | |
|
erweitern Sie dann beide Brüche auf diesen Hauptnenner |
6.3) Kürzen von Bruchtermen
|
ermitteln Sie zunächst den größten gemeinsamen Teiler (ggT) von Zähler und Nenner (gegebenenfalls durch geschicktes Ausklammern) | |
|
kürzen
sie dann gemeinsame Faktoren in Zähler und Nenner |
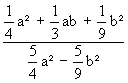 =
=
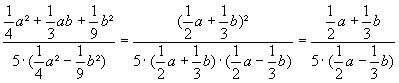
6.4)
Vereinfachung von Bruchtermen, Polynomdivision
Aufgabe:
Vereinfachen Sie den Bruchterm durch Zerlegen von Zähler und Nenner in
Faktoren und anschließendes Kürzen!
|
Verfahren
der Polynomdivision siehe Arbeitblatt
|
7.1)
Addition gleichnamiger Bruchterme
|
Zähler addieren,
Nenner beibehalten |
7.2) Addition ungleichnamiger Bruchterme
|
ermitteln Sie zunächst das kleinste gemeinsame Vielfache (kgV) der beiden Nenner (Hauptnenner) | |
|
erweitern sie dann beide Brüche auf den gemeinsamen Hauptnenner | |
|
addieren
sie nun die gleichnamigen Brüche |
7.3)
Multiplikation von Bruchtermen
|
multiplizieren
Sie zunächst Zähler mit Zähler und Nenner mit Nenner | |
|
kürzen
sie dann gemeinsame Faktoren in Zähler und Nenner und vereinfachen Sie den
Bruch |
7.4) Division von Bruchtermen
|
ersetzen
Sie zunächst die Division mit dem 2.Bruch (Divisor) durch eine Multiplikation
mit dessen Reziproken | |
|
gehen
sie nun vor wie beim Multiplizieren zweier Brüche |
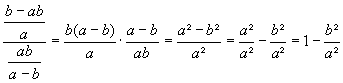
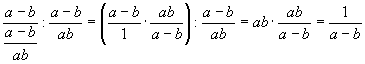
8.)
Lineare Gleichungen und Bruchgleichungen
8.1)
Grundbereich, Definitionsbereich und Lösungsmenge
|
Bestimmen Sie den Definitionsbereich und die Lösungsmenge der Gleichung jeweils für den Grundbereich der rationalen Zahlen Q, der ganzen Zahlen Z und der natürlichen Zahlen N! |
![]() =
2
DB = {x
=
2
DB = {x![]() R|x≠0}
x = 4
LQ = {4}
LZ = {4}
LN = {4}
R|x≠0}
x = 4
LQ = {4}
LZ = {4}
LN = {4}
![]() =
=
![]() DB = {x
DB = {x![]() R|x≠2
und x≠0,25} x
= 1 LQ
= {1}
LZ
= {1}
LN = {1}
R|x≠2
und x≠0,25} x
= 1 LQ
= {1}
LZ
= {1}
LN = {1}
![]() =
1
DB = {x
=
1
DB = {x![]() R|x≠0,75} x = -1
LQ
= {-1}
LZ
= {-1}
LN = Ø
R|x≠0,75} x = -1
LQ
= {-1}
LZ
= {-1}
LN = Ø
8.2)
Bestimmung der Lösungsmenge einfacher Gleichungen
1.
5x + 7 =
3x + 25 /-3x
2x +
7 =
25 /-7
2x =
18 /:2
x = 9
x = 6,8 ![]()
3.
2x – 9( 3x + 1 ) =
3( x – 7 ) + 5( x + 2 )
2x – 27x – 9 = 3x – 21 + 5x
+ 10
-25x – 9 = 8x – 11
/+25x
-9 =
33x – 11 /+11
2 =
33x /:33
![]() ( 0,0606)
( 0,0606)![]() (3,40909)
(3,40909)
5.
13( 2x – 6 ) – 5( 3 + x ) =
4( 23 – 4x ) + 2( x – 7 ) + 7( x – 13 )
26x – 78 – 15 – 5x
= 92 – 16x + 2x – 14 +
7x – 91
21x – 93 =
-7x – 13 /+7x
28x – 93 =
-13 /+93
28x
= 80 /:28
x =
![]() (2,857142)
(2,857142)
6.
1,5( x – 4 ) -
0,5·
( 7 – 8x ) =
0,75·
( 16x – 7 ) – 8( 12x + 0,5 ) + 74,5x
1,5x – 6 – 3,5 + 4x =
12x – 5,25 - 96x – 4 + 74,5x
5,5x – 9,5 =
-9,5x – 9,25 /+9,5x
15x – 9,5 =
-9,25 /+9,5
15x =
0,25 /:15
x =
![]() (0,0166)
(0,0166)
7.
( x – 7 )² - 15( x + 7 ) =
( x – 2 )( x + 2 ) – 5( 3 + 4x ) + 8x
x² - 14x + 49 –15x – 105 =
x² - 4 – 15 – 20x + 8x
x² - 29x – 56 = x² - 12x –
19 /-x²
- 29x – 56 = -12x –
19 /+29x + 19
- 37 =
17x
x =
![]() (-2,176470588)
(-2,176470588)
8.
3x( x – 5 ) + 2( 3 – 2x )²
= 2x( 9 + 2x ) + ( 5 – 3x
)( 2 – 5x ) – 8x²
3x² - 15x + 2( 9 – 12x + 4x² ) = 18x + 4x² + 10 – 25x – 6x + 15x²
- 8x²
3x² - 15x + 18 – 24x + 8x² =
18x + 4x² + 10 – 25x – 6x + 15x² - 8x²
11x² - 39x + 18 =
11x² - 13x + 10 /-11x²
- 39x + 18 =
- 13x + 10 /+39x -10
+ 8 =
26x /:26
x =
![]() (0,307692)
(0,307692)
9.
( x – 5 )( 5 – x ) – 4x( 2 – x )
= ( 7x – 2 )( x + 5 ) –
2x( 2x + 3 )
5x
– x² - 25 + 5x – 8x + 4x² = 7x² + 35x –
2x – 10 – 4x² - 6x
3x² + 2x – 25 =
3x² + 27x – 10 /-3x²
2x – 25 =
27x – 10 /-2x + 10
-15
= 25x
/:25
x =
![]() (-0,6)
(-0,6)
10.
5x( x – 2 )² +
0,2·
( 4x – 2 )( 8 – 5x ) + 5x =
2( 6x + 4 )( 7 – 2x ) – x( 7 – 5x² )
5x( x² - 4x + 4 ) + 0,2·( 32x – 20x² - 16 + 10x ) + 5x = 2( 42x – 12x²
+ 28 – 8x ) – 7x + 5x³
5x³ - 20x² + 20x + 6,4x – 4x² - 3,2 + 2x + 5x
= 84x – 24x² + 56 – 16x
– 7x + 5x³
5x³ - 24x² + 33,4x – 3,2 =
5x³ - 24x² + 61x + 56 /-5x³
-24x² + 33,4x – 3,2 =
-24x² + 61x + 56 /+24x²
33,4x – 3,2 =
61x + 56 /-33,4x - 56
-59,2 =
27,6x /:27,6
11.
4 -
![]() = 3 -
= 3 -
![]() /·20
/·20
4·20
-
![]() = 3·20 -
= 3·20 -
![]()
80 - 4·( 7 – 3x ) =
60 - 2·( 3 – 7x ) + 10·( x + 1 )
80
– 28 + 12x =
60 – 6 + 14x + 10x + 10
12x + 52 =
24x + 64 /-24x
-12x + 52 =
64 /-52
-12x =
12 /:( -12)
x =
-1
Probe: 2
= 2 w.A.
12.
![]() - 4 =
1 -
- 4 =
1 -
![]() /·12
/·12
![]() - 12·4
= 12·1 -
- 12·4
= 12·1 -
![]()
4·( 4x – 1 ) – 48 =
12 - 2·( x – 4 ) + 3·( 3x + 5 ) - 3·17
16x – 4 – 48 =
12 – 2x + 8 + 9x + 15 – 51
16x – 52 =
7x – 16 /-7x
9x – 52 =
-16 /+52
9x = 36
/:9
x = 4 Probe: 1 = 1 w.A.
13.
![]() + 6
=
+ 6
= ![]() /·30
/·30
![]() ·( x + 3 ) + 30·6 =
·( x + 3 ) + 30·6 =
![]()
10·( 7x – 2 ) - 24·( x + 3 ) + 180
= 45·( x + 2 )
70x – 20 – 24x - 72 + 180 =
45x + 90
46x – 88 =
45x + 90 /-45x
x + 88 =
90 /-88
x =
2
Probe: 6
= 6 w.A.
14.
![]() / ·120
/ ·120
![]()
8·( 2x – 3 ) - 6·( 4x – 9 ) =
4·( 8x – 27 ) – 5·( 16x – 81 ) - 3·9
16x – 24 – 24x + 54 = 32x –108 –
80x + 405 – 27
-8x + 30 =
-48x + 270 /+48x
40x
+ 30 = 270
/-30
40x =
240 /:40
x =
6
Probe:
![]() w.A.
w.A.
8.3)
Bruchgleichungen
·
Ermitteln Sie die Lösungsmenge
folgender Bruchgleichungen, in dem Sie:
-
den Definitionsbereich bestimmen
-
mit dem Hauptnenner beide Seiten
multiplizieren
-
die bruchfreie Gleichung lösen
-
überprüfen, ob die Lösung im
Definitionsbereich liegt
- eine Probe in der Ausgangsgleichung machen
1.
![]() = -
= -
![]() - 33 /·4x
DB = { x
- 33 /·4x
DB = { x
![]() R |
x ≠ 0}
R |
x ≠ 0}
5 = -28 – 132x /+28
33 = - 132x
x = -1/4 = -0,25
Probe: -5 = -5 w.A.
L = {-1/4}
2.
![]() =
=
![]() /·(2-x)(3-x)
DB = { x
/·(2-x)(3-x)
DB = { x
![]() R |
x ≠ 2 und x ≠ 3 }
R |
x ≠ 2 und x ≠ 3 }
3·(3
– x) = 2·(2 – x)
9 – 3x = 4 – 2x /+3x /-4
5 = x
Probe: -1 = -1 w.A.
L = {5}
3.
![]() +
+
![]() =
=
![]() /·(2-3x)(x+3)
DB = { x
/·(2-3x)(x+3)
DB = { x
![]() R |
x ≠ 2/3 und x ≠ -3 }
R |
x ≠ 2/3 und x ≠ -3 }
x + 3
+ 2·(2 – 3x) = 3·(2 – 3x)
7 – 5x = 6 – 9x /+9x – 7
4x = -1
x = -1/4 = -0,25
Probe: 12/11 = 12/11 w.A.
L = {-1/4}
4.
![]() =
=
![]() + 3 /·2(2-x)
DB = { x
+ 3 /·2(2-x)
DB = { x
![]() R |
x ≠ 2}
R |
x ≠ 2}
7 = 10 + 3·(4 – 2x)
7 = 22 – 6x /+6x – 7
6x = 15
x = 5/2 = 2,5
Probe: -7 = -7 w.A.
L = {5/2}
5.
![]() +
+
![]() =
2 /·(2+x)(3-x)
DB = { x
=
2 /·(2+x)(3-x)
DB = { x
![]() R |
x ≠ -2 und x ≠ 3 }
R |
x ≠ -2 und x ≠ 3 }
2x·(3
– x) + 3·(2 + x) = 2·(2 + x)(3 – x)
6x – 2x² + 6 + 3x = 2·(6 + x – x²)
-2x² + 9x + 6 = -2x² + 2x + 12 /+2x²
9x + 6 = 2x + 12 /-2x – 6
7x = 6
x = 6/7
Probe: 2 = 2 w.A.
L = {6/7}
6.
![]() =
=
![]() /·6(3x+2)
DB = { x
/·6(3x+2)
DB = { x
![]() R |
x ≠ -2/3 }
R |
x ≠ -2/3 }
3·(7x
– 4) = 2·(5x – 6)
21x – 12 = 10x – 12 /-10x + 12
11x = 0
x = 0
Probe: -1 = -1 w.A.
L = {0}
7.
![]() -
-
![]() =
=
![]() -
-
![]() /·2(3+x)(2+x)
DB = { x
/·2(3+x)(2+x)
DB = { x
![]() R |
x ≠ -3 und x ≠ -2 }
R |
x ≠ -3 und x ≠ -2 }
8·(2
+ x) – 14·(3 + x) = 3·(3 + x) – 5(2 + x)
16 +
8x – 42 – 14x = 9 + 3x – 10 – 5x
-6x – 26 = -2x – 1 /+6x + 1
-25 = 4x
x = -25/4 = -6,25 Probe:
92/221 = 92/221 w.A.
L = {-25/4}
8.
![]() =
=
![]() +
+
![]() /·(x+7)(x-7)
DB = { x
/·(x+7)(x-7)
DB = { x
![]() R |
x ≠ 7 und x ≠ -7 }
R |
x ≠ 7 und x ≠ -7 }
(3 +
x)(x + 7) = x² + 9·(x – 7)
x² +
10x + 21 = x² + 9x – 63 /-x²
10x + 21 = 9x – 63 /-9x – 21
x = -84
Probe: 81/91 = 81/91 w.A.
L = {-84}
9.
![]() +
+
![]() =
=
![]() /·6(5+x)(5-x)
DB = { x
/·6(5+x)(5-x)
DB = { x
![]() R |
x ≠ 5 und x ≠ -5 }
R |
x ≠ 5 und x ≠ -5 }
3x·(5
+ x) – 2·(5 – x) =
6·(0,5x² + x)
15x + 3x² - 10 + 2x =
3x² + 6x
3x² + 17x – 10 =
3x² + 6x /-3x²
17x – 10 =
6x /-6x + 10
11x = 10
x = 10/11
Probe: 32/585 = 32/585 w.A.
L = {10/11}
10.
![]() -
-
![]() =
=
![]() -
-
![]() /·2(1-x)(1+x)
DB = { x
/·2(1-x)(1+x)
DB = { x
![]() R |
x ≠ 1 und x ≠ -1 }
R |
x ≠ 1 und x ≠ -1 }
10·(1
+ x) – 6x·(1 – x) =
6x² - 3·(1 – x)
10 + 10x – 6x + 6x² =
6x² - 3 + 3x
6x² + 4x + 10 =
6x² + 3x – 3 /-6x²
4x + 10 =
3x – 3 /-3x – 10
x = -13
Probe: -81/28 = -81/28 w.A.
L = {-13}
11.
![]() -
-
![]() =
=
![]() /·2(5+x)(2-x)
DB = { x
/·2(5+x)(2-x)
DB = { x
![]() R |
x ≠ 2 und x ≠ -5 }
R |
x ≠ 2 und x ≠ -5 }
8x·(2
– x) – 8x·(5 + x) =
16x·(2 – x)
16x – 8x² - 40x – 8x² =
32x – 16x²
-16x² - 24x =
-16x² + 32x /-8x²
-24x =
32x /+24x
0 = 56x /:56
x = 0
Probe: 0 = 0 w.A.
L = {0}
12.
![]() +
+
![]() =
=
![]() +
+
![]() /·3x(x-5)(x+2)
DB = { x
/·3x(x-5)(x+2)
DB = { x
![]() R |
x ≠ 5 und x ≠ -2 und x ≠ 0 }
R |
x ≠ 5 und x ≠ -2 und x ≠ 0 }
9x·(x
+ 2) + 6x·(x – 5) = 12x·(x – 5) + 3·(x² - 3x – 10)
9x²
+ 18x + 6x² - 30x =
12x² - 60x + 3x² - 9x - 30
15x² -12x =
15x² - 69x – 30 /-15x²
-12x =
-69x – 30 /+69x
57x
= -30
x = -10/19 Probe: 57/70 = 57/70 w.A. L = {-10/19}
13.
![]() +
+
![]() =
=
![]() +
+
![]() /·2x(x-3) DB
= { x
/·2x(x-3) DB
= { x
![]() R |
x ≠ 0 und x ≠ 3 }
R |
x ≠ 0 und x ≠ 3 }
2x +
6·(x – 3) = 6·(x – 3) + x
2x
+ 6x – 18 =
6x – 18 + x
8x – 18 = 7x – 18 /-7x
+ 18
x = 0
14.
![]() -
-
![]() =
=
![]() /·7(3+2x)² DB = { x
/·7(3+2x)² DB = { x
![]() R |
x ≠ -3/2 }
R |
x ≠ -3/2 }
7·(3 + 2x) – 7x =
3,5·(3 + 2x)
21 + 14x – 7x =
10,5 + 7x
21 + 7x = 10, 5 + 7x /-7x
– 10,5
10,5 = 0 Widerspruch Probe: nicht möglich L = Ø
15.
![]() +
+
![]() =
=
![]() -
-
![]() /·2x(3+x)(3-x) DB = { x
/·2x(3+x)(3-x) DB = { x
![]() R |
x ≠ 3 und x ≠ -3 und x ≠ 0 }
R |
x ≠ 3 und x ≠ -3 und x ≠ 0 }
4x·(3
– x) + 2x·(3 + x) =
-4x² – 2·(9 – x²)
12x – 4x² + 6x + 2x² =
-4x² – 18 + 2x²
-2x² + 18x =
-2x² - 18 /+2x²
18x = -18
x = -1
Probe: 5/4 = 5/4 w.A.
L = {-1}
9.)
Ungleichungen und Bruchungleichungen
9.1)
Bestimmung der Lösungsmenge einfacher Ungleichungen
- beachten Sie die Unterschiede bei den Äquivalenzumformungen zwischen Gleichungen und Ungleichungen und geben Sie die Lösungsmenge im Bereich der reellen Zahlen an!
1.
3 + 2x
![]() -7 – 3x /+3x – 3
2. 4 + 7x
> 3x – 16 /-3x – 4
-7 – 3x /+3x – 3
2. 4 + 7x
> 3x – 16 /-3x – 4
5x
![]() -10 /:5
4x > -20 /:4
-10 /:5
4x > -20 /:4
x
![]() -2
L = {x
-2
L = {x
![]() R| x
R| x
![]() -2 } x > -5
L = {x
-2 } x > -5
L = {x
![]() R| x > -5 }
R| x > -5 }
3.
13x – 5
![]() 10x + 23 /-10x + 5
4. 25x – 12 <
20x + 28 /-20x + 12
10x + 23 /-10x + 5
4. 25x – 12 <
20x + 28 /-20x + 12
3x
![]() 28 /:3
5x < 30 /:5
28 /:3
5x < 30 /:5
x
![]()
![]() L
= {x
L
= {x
![]() R| x
R| x
![]() 28/3 }
x <
6
L = {x
28/3 }
x <
6
L = {x
![]() R| x < 6 }
R| x < 6 }
5.
3x + 5 <
5x – 7 /-5x - 5
6. x – 3
< 2x + 5 /-2x + 3
-2x < -12 /:(-2)
-x < 8 /·(-1)
x > 6
L = {x
![]() R| x > 6 }
x > -8
L = {x
R| x > 6 }
x > -8
L = {x
![]() R| x > -8 }
R| x > -8 }
7.
2x – 0,2 <
4x + 3 /-4x + 0,2
8. 2x + 2,5
![]() 6x – 1,5 /-2x + 1,5
6x – 1,5 /-2x + 1,5
-2x < 3,2 /:(-2)
4
![]() 4x /:4
4x /:4
x > -1,6
L
= {x
![]() R| x > -1,6 }
x
R| x > -1,6 }
x
![]() 1
L = {x
1
L = {x
![]() R| x
R| x
![]() 1 }
1 }
9.
0,5x – 7
![]() -2x – 8 /+2x + 7
10. –1,5( x – 3 ) + x
-2x – 8 /+2x + 7
10. –1,5( x – 3 ) + x
![]() 2x -
2x -
![]()
![]() x
x
![]() -1 /·
-1 /·
![]() -1,5x + 4,5 + x
-1,5x + 4,5 + x
![]() 2x -
2x -
![]()
x
![]() -
-![]() L = {x
L = {x
![]() R|
x
R|
x
![]() -2/5
}
-0,5x
-2/5
}
-0,5x
![]() 2x
-
2x
-
![]() /-2x
/-2x
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-
![]() x
x
![]() -
-![]() /·(-
/·(-![]() )
)
-4 -3
-2 -1
0 1
2 3
x
![]()
![]() L = {x
L = {x
![]() R|
x
R|
x
![]() 3/20 }
3/20 }
Die
Lösungsmenge einer Ungleichung ist in der Regel eine unendlich große
Zahlenmenge, die durch einen bestimmten Bereich auf der Zahlengerade
veranschaulicht werden kann.
9.2)
Bruchungleichungen
Bestimmen
Sie die Lösungsmenge der Bruchungleichungen, in dem Sie:
-
den Definitionsbereich der
Ungleichung ermitteln
-
die Ungleichung mit dem Hauptnenner
durchmultiplizieren
-
dabei eine Fallunterscheidung
vornehmen für den Fall, dass der Hauptnenner größer(gleich) Null bzw. dass
der Hauptnenner kleiner als Null ist
-
die entstandenen Teilungleichungen
lösen und mit der Fallbedingung vergleichen
-
die Gesamtlösungsmenge aus den Lösungsmengen
der beiden Teilungleichungen zusammensetzen und graphisch veranschaulichen
-
mit geeigneten ganzen Zahlen aus
der Lösungsmenge eine Probe machen
1.
![]() >
0 /·x
DB =
{ x
>
0 /·x
DB =
{ x
![]() R| x ≠ 0}
R| x ≠ 0}
x < 0
x > 0
x + 2
< 0 /-2
x +
2 > 0 /-2
x < -2
x >
-2
L1 = { x
![]() R| x < -2}
L2 = {x
R| x < -2}
L2 = {x
![]() R| x > 0}
R| x > 0}![]()
![]()
-3
-2 -1
0
1
2
3
![]() >
0 /·x DB
= { x
>
0 /·x DB
= { x
![]()
x < 0
x > 0
3 -
x < 0 /+x
3 -
x > 0 /+x
x >
3 x
< 3
L1
= Ø
L2 = {x
![]() R| 0 < x < 3}
L
= {x
R| 0 < x < 3}
L
= {x
![]() R|
0 < x < 3}
R|
0 < x < 3}
![]() 0
/·x
DB = { x
0
/·x
DB = { x
![]() R|
x ≠ 0}
R|
x ≠ 0}
x < 0
x > 0
x -
5
![]() 0 /+5 x -
5
0 /+5 x -
5
![]() 0 /+5
0 /+5
x ![]() 5
x
5
x
![]() 5
5
L1
= Ø L2 = {x
![]() R| 0 < x
R| 0 < x
![]() 5}
5}![]()
![]() 5}
5}
![]()
4.
![]() 0
/·3x DB = { x
0
/·3x DB = { x
![]() R|
x ≠ 0}
R|
x ≠ 0}
x < 0
x > 0
1 - 2x
![]() 0 /+2x 1 - 2x
0 /+2x 1 - 2x
![]() 0 /+2x
0 /+2x
2x
![]() 1 /:2 2x
1 /:2 2x
![]() 1
1
x
![]() 0,5
x
0,5
x
![]() 0,5
0,5
L1
= Ø L2 = {x
![]() R| 0 < x
R| 0 < x
![]() 0,5}
0,5}![]() R|
0 < x
R|
0 < x
![]() 0,5}
0,5}
5.
![]() >
0
DB = { x
>
0
DB = { x
![]() R|
x ≠ 1}
R|
x ≠ 1}
![]() >
0
>
0
3 >
0 L
= {x
![]() R}
R}
6.
![]() 0 /·(x+2)
DB = { x
0 /·(x+2)
DB = { x
![]() R|
x ≠ -2}
R|
x ≠ -2}
x < -2
x > -2
x -
1
![]() 0
/+1
x -
1
0
/+1
x -
1
![]() 0 /+1
0 /+1
x
![]() 1
x
1
x
![]() 1
1
L1 = Ø L2 = {x
![]() R|
-2 < x
R|
-2 < x
![]() 1}
L
= {x
1}
L
= {x
![]() R|
-2 < x
R|
-2 < x
![]() 1}
1}
7.
![]() 0
/·(x-4)
DB = { x
0
/·(x-4)
DB = { x
![]() R|
x ≠ 4}
R|
x ≠ 4}
x < 4
x > 4
2x +
5
![]() 0 /-5
2x +
5
0 /-5
2x +
5
![]() 0
/-5
0
/-5
2x
![]() -5 /:2 2x
-5 /:2 2x
![]() -5 /:2
-5 /:2
x
![]() -2,5
x
-2,5
x
![]() -2,5
-2,5
L1 = { x
![]() R|
x
R|
x
![]() -2,5}
L2 = {x
-2,5}
L2 = {x
![]() R|
x > 4}
L = {x
R|
x > 4}
L = {x
![]() R| x
R| x
![]() -2,5 und x > 4}
-2,5 und x > 4}
8.
![]() <
0
DB = { x
<
0
DB = { x
![]() R| x ≠ -0,5}
R| x ≠ -0,5}
x < -0,5
x > -0,5
2x -
7 > 0 /+7 2x -
7 <
0 /+7
2x >
7 /:2
2x <
7 /:2
x > 3,5
x < 3,5
L1 = Ø
L2 = {x
![]() R| -0,5 < x < 3,5}
L
= {x
R| -0,5 < x < 3,5}
L
= {x
![]() R|
-0,5 < x < 3,5}
R|
-0,5 < x < 3,5}
9.
![]() >
0 /·(5x+2)
DB = {x
>
0 /·(5x+2)
DB = {x
![]() R|
x ≠ -0,4}
R|
x ≠ -0,4}
x < -0,4
x > -0,4
5 -
3x <
0 /+3x
5 -
3x > 0 /+3x
3x > 5 /:3
3x <
5 /:3
x >
![]() x
<
x
<
![]()
L1 = Ø
L2 = {x
![]() R| -0,4 < x <
R| -0,4 < x <
![]() } L
= {x
} L
= {x
![]() R|
-0,4 < x <
R|
-0,4 < x <
![]() }
}
10.
![]() <
2 /·(3-x)
DB = { x
<
2 /·(3-x)
DB = { x
![]() R|
x ≠ 3}
R|
x ≠ 3}
x < 3
x > 3
4x +
5 < 2·(3-x) /+2x - 5
4x +
5 > 6 – 2x
/+2x - 5
6x <
1 /:6
6x >
1 /:6
x <
![]() x
>
x
>
![]()
L1 = { x
![]() R|
x <
R|
x <
![]() }
L2 = { x
}
L2 = { x
![]() R|
x > 3}
L = {x
R|
x > 3}
L = {x
![]() R| x <
R| x <
![]() und x > 3}
und x > 3}
11.
![]() > 3 /·(2x+5)
DB = { x
> 3 /·(2x+5)
DB = { x
![]() R| x ≠
R| x ≠
![]() }
}
x < -2,5
x > -2,5
5 +
x < 3·(2x+5)
/-6x - 5
5 + x >
6x + 15 /-6x - 5
-5x <
10 /:(-5)
-5x >
10 /:(-5)
x > -2
x < -2
L1 = Ø
L2 = {x
![]() R| -2,5 < x < -2}
L
= {x
R| -2,5 < x < -2}
L
= {x
![]() R|
-2,5 < x < -2}
R|
-2,5 < x < -2}
12.
![]() 5 /·(1-x)
DB = { x
5 /·(1-x)
DB = { x
![]() R|
x ≠ 1}
R|
x ≠ 1}
x < 1
x > 1
x -
7
![]() 5·(1-x) /+x
x -
7
5·(1-x) /+x
x -
7
![]() 5 – 5x /+5x + 7
5 – 5x /+5x + 7
6x
![]() 12 /:6
6x
12 /:6
6x
![]() 12 /:6
12 /:6
x
![]() 2 x
2 x
![]() 2
2
L1 = { x
![]() R|
x < 1}
L2 = {x
R|
x < 1}
L2 = {x
![]() R|
x
R|
x
![]() 2}
L = {x
2}
L = {x
![]() R| x < 1 und x
R| x < 1 und x
![]() 2}
2}
13.
![]() 1 /·(3x-5)
DB = { x
1 /·(3x-5)
DB = { x
![]() R| x ≠
R| x ≠
![]() }
}
x < 5/3
x > 5/3
2x -
7
![]() 3x - 5 /-3x + 7
2x - 7
3x - 5 /-3x + 7
2x - 7
![]() 3x - 5 /-3x
+ 7
3x - 5 /-3x
+ 7
-x
![]() 2
-x
2
-x
![]() 2
2
x
![]() -2
x
-2
x
![]() -2
-2
L1 = { x
![]() R| -2
R| -2
![]() x < 5/3}
L2 = Ø
L
= {x
x < 5/3}
L2 = Ø
L
= {x
![]() R|
-2
R|
-2
![]() x < 5/3}
x < 5/3}
14.
![]() -
-
![]() <
0 /·(x²+x)
DB = { x
<
0 /·(x²+x)
DB = { x
![]() R|
x ≠ 0 und x ≠ -1}
R|
x ≠ 0 und x ≠ -1}
x < -1
-1 < x < 0
x > 0
2 + 2x -
x < 0 /-2
2 + 2x -
x > 0 /-2
2 +
2x – x <
0 /-2
x < -2 x >
-2
x <
-2
L1 = { x
![]() R|
x < -2} L2
= {x
R|
x < -2} L2
= {x
![]() R|
-1 < x < 0}
L3 = Ø
L = {x
R|
-1 < x < 0}
L3 = Ø
L = {x
![]() R| x < -2 und -1 < x < 0}
R| x < -2 und -1 < x < 0}
15.
![]() +
+
![]() >
0
DB = { x
>
0
DB = { x
![]() R| x ≠ -2 und x
≠ 3 }
R| x ≠ -2 und x
≠ 3 }
x < -2 -2 < x < 3
x > 3
2(x-3) + 3(x+2) > 0 2x
– 6 + 3x + 6 < 0
5x >
0 /:5
x > 0
x <
0
x >
0
L1 = Ø L2 = {x
![]() R| -2 < x < 0}
L3 = {x
R| -2 < x < 0}
L3 = {x
![]() R| x > 3}
L = {x
R| x > 3}
L = {x
![]() R| -2 < x < 0 und x > 3}
R| -2 < x < 0 und x > 3}
16.
![]() -
-
![]() 0 /·(x+1)(2x+6)
DB = { x
0 /·(x+1)(2x+6)
DB = { x
![]() R| x ≠ -1 und x
≠ -3 }
R| x ≠ -1 und x
≠ -3 }
x < -3 -3 < x < -1
x > -1
2x+6 - 5(x+1)
![]() 0
2x + 6 - 5x - 5
0
2x + 6 - 5x - 5
![]() 0
-3x + 1
0
-3x + 1
![]() 0 /+3x
0 /+3x
3x
![]() 1
3x
1
3x
![]() 1 3x
1 3x
![]() 1
1
x
![]() ⅓
x
⅓
x
![]() ⅓
x
⅓
x
![]() ⅓
⅓
L1 = { x
![]() R| x <-3} L2 = Ø
L3={x
R| x <-3} L2 = Ø
L3={x![]() R|-1<x
R|-1<x
![]() ⅓}
L = {x
⅓}
L = {x
![]() R| x < -3 und -1 < x
R| x < -3 und -1 < x
![]() ⅓}
⅓}
17.
![]() +
+
![]() > 0 /·(3x+5)(2x-7) DB
= { x
> 0 /·(3x+5)(2x-7) DB
= { x
![]() R| x ≠
R| x ≠
![]() und x ≠
und x ≠
![]() }
}
x < -5/3
-5/3 < x < 3,5
x > 3,5
-2(2x-7) + 4(3x+5) > 0
-4x + 14 + 12x + 20 < 0
8x +34 > 0 /-34
8x >
-34
8x <
-34
8x >
-34 /:8
x > -4,25
x <
-4,25
x >
-4,25
L1 = {x
![]() R| -4,25 < x < -5/3}
L2 = Ø
L3={x
R| -4,25 < x < -5/3}
L2 = Ø
L3={x![]() R|x>3,5} L={x
R|x>3,5} L={x![]() R|-4,25<x<-5/3 und x>3,5}
R|-4,25<x<-5/3 und x>3,5}
18.
![]() -
-
![]() <
0 /·(x-5)(x+3)
DB = { x
<
0 /·(x-5)(x+3)
DB = { x
![]() R| x ≠ -3 und x
≠ 5 }
R| x ≠ -3 und x
≠ 5 }
x < -3
-3 < x < 5
x > 5
2x(x+3) - 2x(x-5) < 0
2x² + 6x - 2x² + 10x > 0
16x <
0 /:16
x <
0
x > 0
x <
0
L1 = {x
![]() R| x < -3} L2 = {x
R| x < -3} L2 = {x
![]() R| 0 < x < 5} L3 = Ø
L = {x
R| 0 < x < 5} L3 = Ø
L = {x
![]() R| x < -3 und 0 < x < 5}
R| x < -3 und 0 < x < 5}
19.
![]() +
+
![]() 3 /·(x-5)(x+1)
DB = { x
3 /·(x-5)(x+1)
DB = { x
![]() R| x ≠ -1 und x
≠ 5 }
R| x ≠ -1 und x
≠ 5 }
x < -1
-1 < x < 5
x > 5
x(x+1)+2x(x-5)
![]() 3(x²-4x-5)
x²+x+2x²-10x
3(x²-4x-5)
x²+x+2x²-10x
![]() 3x²-12x-15
-9x
3x²-12x-15
-9x
![]() -12x-15
/+12x
-12x-15
/+12x
3x
![]() -15
3x
-15
3x
![]() -15
3x
-15
3x
![]() -15
-15
x
![]() -5
x
-5
x
![]() -5 x
-5 x
![]() -5
-5
L1
= {x
![]() R| -5
R| -5
![]() x < -1}
L2 = Ø L3={x
x < -1}
L2 = Ø L3={x
![]() R|x>5} L
= {x
R|x>5} L
= {x
![]() R|-5
R|-5
![]() x<-1 und
x>5}
x<-1 und
x>5}
20.
![]() +
+
![]() >
>
![]() /·2(x+1)(x-2)
DB = { x
/·2(x+1)(x-2)
DB = { x
![]() R| x ≠ -1 und x
≠ 2 }
R| x ≠ -1 und x
≠ 2 }
x < -1
-1 < x < 2
x > 2
2x(x-2)+2x(x-2)>(2x+1)(2x+2)
2x²–4x+2x²-4x<4x²+6x+2
-8x >
6x + 2 /-6x
-14x > 2 -14x < 2 -14x > 2 /:(-14)
x <
-1/7
x >
-1/7
x <
-1/7
L1
= {x
![]() R| x < -1}
L2 = {x
R| x < -1}
L2 = {x
![]() R| -1/7 < x < 2}
L3 = Ø L
= {x
R| -1/7 < x < 2}
L3 = Ø L
= {x
![]() R|x<-1 und -1/7<x<2}
R|x<-1 und -1/7<x<2}
10.)
Absolutbetrag, Gleichungen und Ungleichungen
10.1)
Der Absolutbetrag
- bestimmen Sie – falls möglich – den Betrag oder geben Sie unter Nutzung einer Fallunterscheidung den vereinfachten Term ohne Betragstriche an!
1.
| - 13,5 | = 13,5
2.
| x – 3 | = x – 3
falls x
![]() 3
| x – 3 | = -x + 3
= 3 – x
falls x < 3
3
| x – 3 | = -x + 3
= 3 – x
falls x < 3
3.
| x + 4 | = x + 4 falls
x
![]() -4
| x + 4 | = -x - 4
falls x < -4
-4
| x + 4 | = -x - 4
falls x < -4
4.
| 6 – x | = 6 – x falls
x
![]() 6
| 6 – x | = -6 + x = x
– 6 falls x > 6
6
| 6 – x | = -6 + x = x
– 6 falls x > 6
5.
| (-2)· 4 | = | -8 |
= 8
6.
| - x² | = x² für
alle x
![]() R , weil –x² in jedem
Fall negativ, höchstens Null ist
R , weil –x² in jedem
Fall negativ, höchstens Null ist
7.
![]() =
=
![]()
8.
![]() =
=
![]() falls x > 0
falls x > 0
![]() = -
= -
![]() falls x < 0
falls x < 0
![]() = nicht definiert für x = 0
= nicht definiert für x = 0
9.
| 5x | = 5x falls x
![]() 0
| 5x | = -5x falls x < 0
0
| 5x | = -5x falls x < 0
10.
| -3x | = 3x falls
x
![]() 0
| -3x | = -3x falls x < 0
0
| -3x | = -3x falls x < 0
11.
![]() =
=
![]() falls x
falls x
![]() -3
-3
![]() =
=
![]() falls x <-3
falls x <-3
12.
![]() =
=
![]() falls –1
falls –1
![]() x<2
x<2
![]() =
=
![]() falls x<-1 bzw. falls x>2
falls x<-1 bzw. falls x>2
![]() für
x = 2 nicht definiert
für
x = 2 nicht definiert
10.2)
Gleichungen mit Absolutbeträgen
Lösen
Sie die Betragsgleichungen in dem Sie:
-
wenn nötig den Definitionsbereich
einschränken
-
mittels Betragsdefinition eine
Fallunterscheidung vornehmen und die Teilgleichungen lösen
-
die Lösungsmenge aus den Teillösungen
zusammensetzen und eine Probe machen
1.
| x | =
5
x < 0
x
![]() 0
0
-x = 5
x = 5
x = -5
L = { -5; 5}
2.
| x – 1 | = 5
x < 1
x
![]() 1
1
-(x - 1) = 5
x - 1 = 5 /+1
-x + 1 = 5 /-1
x = 6
-x = 4
x
= -4
L = { -4; 6}
5 Einheiten
5 Einheiten

Lösung sind die zwei Zahlen, die auf der Zahlengerade von der Zahl 1 den Abstand 5 haben
3.
| x – 1 | + 1 = 5 /-1
| x – 1 | = 4
x < 1
x
![]() 1
1
-x + 1 = 4 /-1
x - 1 = 4 /+1
-x = 3
x = 5
x = -3
L = { -3; 5}
4.
| 4x + 1 | = 3
x < -1/4
x
![]() -1/4
-1/4
-4x - 1 = 3 /+1
4x + 1 = 3 /-1
-4x = 4
4x = 2
x = -1
x = 0,5
L = { -1; 0,5}
5.
| 4 – 5x | = 7
x < 0,8
x
![]() 0,8
0,8
4 – 5x = 7 /-4
-4 + 5x = 7 /+4
-5x = 3 5x = 11
x = -3/5 x = 11/5 L = { -0,6; 2,2}
6.
![]() =
4 /·(2-x)
DB = { x
=
4 /·(2-x)
DB = { x
![]() R| x ≠ 2 }
R| x ≠ 2 }
| x + 5 | = 8 – 4x
x < -5
x
![]() -5
-5
-x - 5 = 8 – 4x /+4x + 5
x + 5 = 8 – 4x /+4x - 5
3x = 13 5x = 3
x = 13/3 (Scheinlösung) x = 3/5 L = { 0,6 }
7.
![]() =
-1 /·|5-x|
DB = { x
=
-1 /·|5-x|
DB = { x
![]() R| x ≠ 5 }
R| x ≠ 5 }
4x - 5 =
- | 5 – x |
x
![]() 5
x > 5
5
x > 5
4x - 5 = -5 + x /-x + 5
4x - 5 = 5 – x /+x + 5
3x = 0 5x = 10
x = 0 x = 2 (Scheinlösung) L = { 0 }
8.
![]() =
0 /·(x-1,5) DB
= { x
=
0 /·(x-1,5) DB
= { x
![]() R| x ≠ 1,5 }
R| x ≠ 1,5 }
| 2x – 3 | = 0
x <
1,5
x
![]() 1,5
1,5
-2x + 3 = 0 /+2x
2x - 3 = 0 /+3
3 = 2x 2x = 3
x = 1,5
![]() DB x = 1,5
DB x = 1,5
![]() DB
L = Ø
DB
L = Ø
9.
![]() =
2
DB = { x
=
2
DB = { x
![]() R| x ≠ 2 }
R| x ≠ 2 }
![]() = 2 /·|x-2|
= 2 /·|x-2|
| x – 1 | = 2· | x – 2 |
x < 1
1
![]() x < 2
x
x < 2
x
![]() 2
2
-x + 1 = -2x + 4 /+2x-1 x - 1 = -2x + 4 /+2x+1
x – 1 = 2x – 4 /-2x + 1
3x = 3 3x = 5 -x = -3
x = 1 (Scheinlösung) x = 5/3 x = 3 L = {5/3 ; 3}
10.
 =
3 /·|4+x|
DB = { x
=
3 /·|4+x|
DB = { x
![]() R| x ≠ -4 }
R| x ≠ -4 }
| 20 – 2x | = 3· | 4 + x |
x < -4
-4
![]() x < 10
x
x < 10
x
![]() 10
10
20 – 2x = -12 – 3x
/+3x-20 20 – 2x = 12 + 3x /-3x-20
-20 + 2x = 12 + 3x /-3x + 20
x = -32 -5x = -8 -x = 32
L = {-32; 8/5 }
x
= 8/5
x = -32 (Widerspruch)
11.
| x + 3 | + 2 = | x – 7 |
x < -3
-3
![]() x < 7
x
x < 7
x
![]() 7
7
-x – 3 + 2 = -x + 7 /+x+1
x + 3 + 2 = -x + 7 /+x-5
x + 3 + 2 = x – 7 /-x + 5
0 = 8 (Widerspruch) 2x = 2 0 = -2 (Widerspruch)
x = 1
L = { 1 }
12.
| x + 2 | - 4 = | x – 3 |
x <
-2
-2
![]() x < 3
x
x < 3
x
![]() 3
3
-x – 2 - 4 = -x + 3 /+x+6
x + 2 - 4 = -x + 3 /+x+2
x + 2 - 4 = x – 3 /-x + 2
0 = 9 (Widerspruch) 2x = 5 0 =-1 (Widerspruch)
x = 2,5 L = { 2,5 }
13.
| x | + | x – 1 | =
7
x < 0
0
![]() x < 1
x
x < 1
x
![]() 1
1
-x – x + 1 = 7 /-1
x
- x + 1 = 7 /-1
x + x - 1 = 7 /+1
-2x = 6 0 = 6 (Widerspruch) 2x = 8
x = -3 L = { -3 ; 4 } x = 4
14.
3| x | + | 4x – 2 | =
5
x < 0
0
![]() x < 0,5
x
x < 0,5
x
![]() 0,5
0,5
-3x – 4x + 2 = 5 /-2 3x
- 4x + 2 = 5 /-2
3x + 4x - 2 = 5 /+2
-7x = 3 -x = 3 7x = 7
x = -3/7 x = -3 (Scheinlösung) x = 1 L = { -3/7 ;1 }
15.
| x + 5 | + | x – 4 | =
-3
x < -5 -5
![]() x < 4
x
x < 4
x
![]() 4
4
-x – 5 – x + 4 = -3 /+1 x + 5 - x + 4 = -3 /+9
x + 5 + x - 4
= -3 /-1
-2x = -2
0 = 9 (Widerspruch)
2x =
-4
10.3)
Ungleichungen mit Absolutbeträgen
Lösen
Sie die Betragsungleichungen in dem Sie:
-
wenn nötig den Definitionsbereich
einschränken
-
mittels Betragsdefinition eine
Fallunterscheidung vornehmen und die Teilungleichungen lösen
-
die Lösungsmenge aus den Teillösungen
zusammensetzen und mit geeigneten ganzen Zahlen aus der Lösungsmenge eine Probe machen
1.
| x |
![]() 2
2
x <
0
x
![]() 0
0
-x
![]() 2 /·(-1)
x
2 /·(-1)
x
![]() 2
2
x
![]() -2
L2 = { x
-2
L2 = { x
![]() R;
x
R;
x
![]() 2 }
2 }
L1 = { x
![]() R;
x
R;
x
![]() -2 }
L = { x
-2 }
L = { x
![]() R;
x
R;
x
![]() -2 und x
-2 und x
![]() 2 }
2 }
2.
| x |
![]() 1
1
x <
0
x
![]() 0
0
-x
![]() 1 /·(-1)
x
1 /·(-1)
x
![]() 1
1
x
![]() -1
L2 = { x
-1
L2 = { x
![]() R;
x
R;
x
![]() 1 }
1 }
L1 = { x
![]() R;
x
R;
x
![]() -1 }
L = { x
-1 }
L = { x
![]() R;
-1
R;
-1
![]() x
x
![]() 1 }
1 }
3.
| x – 4 | < 2
x <
4
x
![]() 4
4
-x + 4 < 2 /-4
x
– 4 < 2 /+4
-x < -2
x < 6
x > 2
L2 = { x
![]() R;
x < 6 }
R;
x < 6 }
L1 = { x
![]() R;
x > 2 }
L = { x
R;
x > 2 }
L = { x
![]() R;
2 < x < 6 }
R;
2 < x < 6 }
![]()
0 1 2 3 4 5 6 7 8 9
Zur Lösungsmenge gehören alle Zahlen, die von der Zahl 4 einen
kleineren Abstand
als 2 haben.
4.
| x + 4 | <
2
x < -4
x
![]() -4
-4
-x - 4 < 2 /+4
x
+ 4 < 2 /-4
-x < 6 /·(-1)
x < -2
x > -6
L2 = { x
![]() R;
x < -2 }
R;
x < -2 }
L1 = { x
![]() R;
x > -6 } L
= { x
R;
x > -6 } L
= { x
![]() R;
-6 < x < -2 }
R;
-6 < x < -2 }
5.
| x – 4 |
![]() 2
2
x < 4
x
![]() 4
4
-x + 4
![]() 2 /-4
x
– 4
2 /-4
x
– 4
![]() 2 /+4
2 /+4
-x
![]() -2/·(-1)
x
-2/·(-1)
x
![]() 6
6
x
![]() 2
L2 = { x
2
L2 = { x
![]() R;
x
R;
x
![]() 6 }
6 }
L1 = { x
![]() R;
x > 2 }
L = { x
R;
x > 2 }
L = { x
![]() R;
x
R;
x
![]() 2 und x
2 und x
![]() 6
}
6
}
6.
| 2x – 7 |
![]() 2
2
x < 3,5
x
![]() 3,5
3,5
-2x + 7
![]() 2 /-7
2x – 7
2 /-7
2x – 7
![]() 2 /+7
2 /+7
-2x
![]() -5 /:(-2)
2x
-5 /:(-2)
2x
![]() 9 /:2
9 /:2
x
![]() 2,5
L2 = { x
2,5
L2 = { x
![]() R;
x
R;
x
![]() 4,5 }
4,5 }
L1 = { x
![]() R;
x
R;
x
![]() 2,5}
L = { x
2,5}
L = { x
![]() R;
2,5
R;
2,5
![]() x
x
![]() 4,5 }
4,5 }
7.
| x + 2 | + 1
![]() | x – 2 |
| x – 2 |
x < -2
-2
![]() x
< 2
x
x
< 2
x
![]() 2
2
-x - 2 + 1
![]() -x + 2 /+x+1 x + 2 + 1
-x + 2 /+x+1 x + 2 + 1
![]() -x + 2 /+x-3
x + 2 + 1
-x + 2 /+x-3
x + 2 + 1
![]() x - 2 /-x-3
x - 2 /-x-3
0
![]() 3 w.A. 2
x
3 w.A. 2
x
![]() -1 /:2
0
-1 /:2
0
![]() -5 (Widerspruch)
-5 (Widerspruch)
x < -2
x
![]() -0,5
L3 = Ø
-0,5
L3 = Ø
L1 = { x
![]() R;
x < -2} L2
= {x
R;
x < -2} L2
= {x
![]() R;
-2
R;
-2
![]() x
x
![]() -0,5 } L = { x
-0,5 } L = { x
![]() R;
2,5
R;
2,5
![]() x
x
![]() 4,5 }
4,5 }
8.
| 2x – 5 |
![]() | x + 1 | + 2
| x + 1 | + 2
x < -1
-1
![]() x < 2,5
x
x < 2,5
x
![]() 2,5
2,5
-2x + 5
![]() -x – 1 + 2 /+x-5 -2x + 5
-x – 1 + 2 /+x-5 -2x + 5
![]() x + 1 + 2 /-x-5
2x - 5
x + 1 + 2 /-x-5
2x - 5
![]() x + 1 + 2 /-x+5
x + 1 + 2 /-x+5
-x
![]() -4 /·(-1) - 3x
-4 /·(-1) - 3x
![]() -2 /:(-3)
x
-2 /:(-3)
x
![]() 8
8
x
![]() 4
x
4
x
![]() 2/3
L3 = {x
2/3
L3 = {x
![]() R; 2,5
R; 2,5
![]() x
x
![]() 8 }
8 }
L1 = Ø
L2 = {x
![]() R; 2/3
R; 2/3
![]() x < 2,5 } L
= { x
x < 2,5 } L
= { x
![]() R; 2/3
R; 2/3
![]() x
x
![]() 8 }
8 }
9.
| x | + 1
![]() | x – 5 |
| x – 5 |
x <
0
0
![]() x < 5
x
x < 5
x
![]() 5
5
-x + 1
![]() -x + 5 /+x-1
x + 1
-x + 5 /+x-1
x + 1 ![]() -x + 5 /+x-1
x + 1
-x + 5 /+x-1
x + 1
![]() x - 5 /+x-1
x - 5 /+x-1
0
![]() 4 /·(-1)
2x
4 /·(-1)
2x
![]() 4
/:2
0
4
/:2
0
![]() -6
-6
L1
= Ø
x
![]() 2
L3 = Ø
2
L3 = Ø
L2 = {x
![]() R; 2
R; 2
![]() x
< 5 } L
= { x
x
< 5 } L
= { x
![]() R; 2
R; 2
![]() x < 5 }
x < 5 }
10.
![]() <
4 /·2x
DB = { x
<
4 /·2x
DB = { x
![]() R ;
x ≠ 0}
R ;
x ≠ 0}
x
< 0
x
![]() 0
0
|
3x – 5 | > 8x
| 3x – 5 | < 8x
0
![]() x
< 5/3 x
x
< 5/3 x
![]() 5/3
5/3
-3x + 5 > 8x
/+3x
-3x + 5 < 8x /+3x
3x - 5 < 8x /-3x
5 > 11x / :11
5 < 11x /:11
-5 < 5x
x < 5/11 x > 5/11 x > -1
L1 = {x
![]() R; x < 0 }
L2 = {x
R; x < 0 }
L2 = {x
![]() R; 5/11 < x < 5/3 }
L3 = {x
R; 5/11 < x < 5/3 }
L3 = {x
![]() R; x
R; x
![]() 5/3 }
5/3 }
L
= { x
![]() R;
x < 0 und 5/11
R;
x < 0 und 5/11
![]() x < ∞ }
x < ∞ }
11.
![]() >
5 /·x
DB = { x
>
5 /·x
DB = { x
![]() R ;
x ≠ 0}
R ;
x ≠ 0}
x < 0
x
![]() 0
0
| 4x + 2 | < 5x
| 4x + 2 | > 5x
∞ < x
< -0,5
-0,5
![]() x < 0
x < 0
-4x - 2 < 5x /+4x
4x + 2 < 5x /-4x
4x + 2 > 5x /-4x
-2 < 9x / :9
2 < x
2 > x
x > -2/9 x > 2 x < 2
L1 = Ø
L2
= Ø
L3 = {x
![]() R;
0 < x < 2 }
L = { x
R;
0 < x < 2 }
L = { x
![]() R;
0
R;
0
![]() x < 2 }
x < 2 }
12.
![]() <
6 /·0,5x
DB = { x
<
6 /·0,5x
DB = { x
![]() R ;
x ≠ 0}
R ;
x ≠ 0}
x < 0
x
![]() 0
0
| x – 4 | > 3x
| x – 4 | < 3x
0
![]() x < 4
x
x < 4
x
![]() 4
4
-x + 4 > 3x /+x
-x + 4 < 3x /+x
x - 4 < 3x /-x
4 > 4x / :4
4 < 4x /:4 -4 < 2x
x < 1 x > 1 x > -2
L1 = {x
![]() R;
x < 0 }
L2 = {x
R;
x < 0 }
L2 = {x
![]() R;
1 < x < 4 }
L3 = {x
R;
1 < x < 4 }
L3 = {x
![]() R;
x
R;
x
![]() 4}
L={x
4}
L={x
![]() R;x<0
und 1
R;x<0
und 1
![]() x<∞}
x<∞}
14.) Funktionslehre
14.1) Lineare Funktionen
-
Aufgabe:
Geben Sie die Steigung der Geraden an! Bestimmen Sie jeweils die Schnittpunkte
1.
f(x) =
y = 2x – 1
m = 2
Sx(0,5|0)
Sy(0|-1)
2.
f(x) =
y = -3x +
![]() m = -3
Sx(0,5|0)
Sy(0|1,5)
m = -3
Sx(0,5|0)
Sy(0|1,5)
3.
f(x) =
y =
![]() x -
x -
![]() m = 2,5
Sx(0,2|0)
Sy(0|-0,5)
m = 2,5
Sx(0,2|0)
Sy(0|-0,5)
4.
f(x) =
y = -
![]() x
m = -0,5
Sx(0|0)
Sy(0|0)
x
m = -0,5
Sx(0|0)
Sy(0|0)
5.
f(x) =
y = -
![]() x + 1
m = -0,25
Sx(4|0)
Sy(0|1)
x + 1
m = -0,25
Sx(4|0)
Sy(0|1)
6.
f(x) =
y =
![]() x + 3
m = 2/3
Sx(-4,5|0)
Sy(0|3)
x + 3
m = 2/3
Sx(-4,5|0)
Sy(0|3)
7.
f(x) =
y =
![]() x + 3
m = -1,5
Sx(2|0)
Sy(0|3)
x + 3
m = -1,5
Sx(2|0)
Sy(0|3)
8.
f(x) =
y = -2
m = 0
keiner
Sy(0|-2)
9.
f(x) =
y = x + 2
m = 1
Sx(-2|0)
Sy(0|2)
10.
f(x) =
y =
![]() x -
x -
![]() m = 0,6
Sx(2/3|0)
Sy(0|-0,4)
m = 0,6
Sx(2/3|0)
Sy(0|-0,4)
14.5)
Quadratische Funktionen
Aufgabe:
Bestimmen Sie jeweils den Scheitel der Parabel und zeichnen Sie den Funktionsgraphen
in ein kartesisches Koordinatensystem!
14.6)
Nullstellen
quadratischer Funktionen
Aufgabe :
Bestimmen Sie die Nullstellen von f
sowie die Koordinaten des Scheitelpunktes der
Parabel und zeichnen Sie den Graph der Funktion!
f(x)
= y
= x² - 1
xN1 =
-1
xN2 = 1
S(0|-1)
f(x)
= y
= x² + 1,5
keine Nullstellen
S(0|1,5)
f(x)
= y = x² + 2x + 1
xN1/2
= -1
S(-1|0)
f(x)
= y
= x² + 5x + 6,25
xN1/2
= -2,5
S(-2,5|0)
f(x)
= y = x² - 8x + 16 xN1/2
= 4
S(4|0)
f(x) = y
= x² + 4x + 3
xN1 =
-3
xN2 = -1 S(-2|-1)
f(x)
= y
= x² - 6x + 11
keine
Nullstellen
S(3|2)
f(x)
= y
= x² + 5x + 7,25
xN1/2
= -2,5
S(-2,5|0)
f(x)
= y
= x² - 3x + 0,25
xN1 =
1,5+√2 xN2 = 1,5-√2
S(1,5|-2)
f(x)
= y
= x² + 6x + 7
xN1 =
-3+√2 xN2 = -3-√2
S(-3|-2)
f(x)
= y
= -x² + 1
xN1 =
-1
xN2 = 1
S(0|1)
f(x)
= y
= -x² - 4
keine
Nullstellen
S(0|-4)
f(x)
= y = -x² - 4x –
4
xN1/2
= -2
S(-2|0)
f(x)
= y
= -x² + 5x – 6,25
xN1/2
= 2,5
S(2,5|0)
f(x)
= y
= -x² + 4x
xN1 =
0
xN2 = 4
S(2|4)
f(x)
= y
= -x² - 2x + 1
xN1 =
-1+√2 xN2 = -1-√2
S(-1|2)
f(x)
= y
=
![]() x² - 2
xN1 =
-2
xN2 = 2
S(0|-2)
x² - 2
xN1 =
-2
xN2 = 2
S(0|-2)
f(x)
= y
=
![]() x² + 1
keine
Nullstellen
S(0|1)
x² + 1
keine
Nullstellen
S(0|1)
f(x)
= y
=
![]() x² - 2,5x + 3,125
xN1/2
= 2,5
S(2,5|0)
x² - 2,5x + 3,125
xN1/2
= 2,5
S(2,5|0)
f(x)
= y
=
![]() x² + 1,5x + 1,125
xN1/2
= -1,5
S(-1,5|0)
x² + 1,5x + 1,125
xN1/2
= -1,5
S(-1,5|0)
f(x)
= y
=
![]() x² - 2x
xN1 =
0
xN2 = 4
S(2|-2)
x² - 2x
xN1 =
0
xN2 = 4
S(2|-2)
f(x)
= y
= -
![]() x² - 2x
xN1 =
0
xN2 = -4 S(-2|2)
x² - 2x
xN1 =
0
xN2 = -4 S(-2|2)
f(x)
= y
= -
![]() x² + x + 4
xN1 =
-2
xN2 = 4
S(1|4,5)
x² + x + 4
xN1 =
-2
xN2 = 4
S(1|4,5)
f(x)
= y
= -
![]() x² + 0,5x + 0,75
xN1 =
-1
xN2 = 3
S(1|1)
x² + 0,5x + 0,75
xN1 =
-1
xN2 = 3
S(1|1)
f(x)
= y
= 2x² - 2
xN1 =
-1
xN2 = 1
S(0|-2)
f(x)
= y
= -2x² + 4
xN1 =
-√2
xN2 = √2 S(0|4)
f(x)
= y
= 2x² + 8x + 8
xN1/2
= -2
S(-2|0)
f(x)
= y
= -2x² + 12x – 18
xN1/2
= 3
S(3|0)
f(x)
= y
= 2x² - 8x + 6
xN1 =
1
xN2 = 3
S(2|-2)
f(x)
= y
= -2x² - 8x – 6
xN1 =
-1
xN2 = -3 S(-2|2)
16.) Absoluter Betrag
16.1) Der absolute Betrag
- bestimmen Sie – falls möglich – den Betrag oder geben Sie unter Nutzung einer Fallunterscheidung den vereinfachten Term ohne Betragstriche an!
17.)
17.1)
Tägliche Übungen - Mathematik Klasse 11-II GK
a) Fassen Sie zusammen: ab2 - 4a2b - 3b2a2 + 5ba + 8b2a - 2a2b2 + 7ba2 = -5a2b2 + 3a2b + 9ab2 + 5ab
b) Berechnen Sie den Wert des Term:
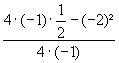 = 1,5
= 1,5
c) Lösen Sie die Gleichung: x2 + 2x - 3 = 0 und prüfen Sie ihr Ergebnis mit dem Satz von Vieta!
x1 = -3 x2 = 1 (-3)·1 = -3 w.A. -3 + 1 = -2 = - (2) w.A.
d) Stellen Sie die Gleichung: V = 0,25π·r2·h nach r um! r = √(4V)/(π·h)
e) Benennen und erläutern Sie den Satz des Thales an einer geeigneten Skizze!
Jeder Peripheriewinkel über dem Durchmesser eines Kreises ist eine rechter Winkel (Sonderfall des Peripheriewinkel-Zentriwinkel-Satzes).
a) Klammern Sie den größtmöglichen Faktor aus: 18x2y - 6xy + 30xy2 = 6xy·(3x - 1 + 5y)
b) Berechnen Sie den Wert des Term:
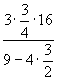 =
12
=
12
c) Lösen Sie die Gleichung: 0,75x2 - 6x + 5,25 = 0 ! x1 = 1 x2 = 7
d) Stellen Sie die Gleichung: Whub = m·g·l·(1 - cosα) nach cosα um!
cosα = 1 - Whub/(m·g·l)
e) Benennen und erläutern Sie den Sinussatz an einer geeigneten Skizze!
a/sinα = b/sinβ = c/sinγ im beliebigen Dreieck liegt der größten Seite auch der größte Winkel gegenüber
a) Formen Sie mittels Binomischer Formeln um: (5x - 1,5)(5x + 1,5) = 25x2 - 2,25 (3.Bin. Formel)
( x2 - x + 0,25) = (x - 0,5)2 (Umkehrung der bin.Formel)
b) Berechnen Sie den Wert des Term:
![]() =
=
![]()
c) Lösen Sie die Gleichung: 0,25x2 + 12,25 = 0 ! x2 = - 49 keine Lösung
d) Stellen Sie die Gleichung: V = 2π r2 + 2π rh nach h um!
V - 2π r2 = 2π rh h = (V - 2π r2)/2π r = V/2π r - r
e) Benennen und erläutern Sie die Winkelbeziehungen für den Sinus, Cosinus und Tangens in einem
rechtwinkligen Dreieck an einer geeigneten Skizze!
sinα = Gegenkathete : Hypotenuse = a/c
cosα = Ankathete : Hypotenuse = b/c
tanα = Gegenkathete : Ankathete = a/b
a) Berechnen Sie für die Funktion f(x) = x2 - 3 den Funktionswert an der Stelle xo + 2
f(xo + 2) = (xo + 2)2 - 3 = xo2 + 4xo + 4 - 3 = xo2 + 4xo + 1
b) Berechnen Sie den Wert der Terme: √1600 = 40 -42 ·3 + 4·(-3)2 = - 48 + 36 = -12
c) Lösen Sie die folgende Gleichung: |x - 4| = 1 Fallunterscheidung:
für x > 4 folgt: x - 4 = 1 x1 = 5
für x < 4 folgt: -(x - 4) = 1 -x + 4 = 1 -x = - 3 x2 = 3
Ergebnis: Lösung sind die zwei Zahlen, die von 4 den Abstand 1 haben !!!
d) Stellen Sie die Gleichung: Q = m1·c·∆T1 + m2·c·∆T2 nach c um!
Grundgedanke: Ausklammern (weil gesuchte Größe in mehreren Termen enthalten) Q = c·(m1·∆T1 + m2·∆T2) c = Q/(m1·∆T1 + m2·∆T2)
e) Benennen und erläutern Sie den Nebenwinkelsatz an einer geeigneten Skizze!
zwei benachbarte Winkel am Schnittpunkt zweier Geraden heißen Nebenwinkel und sind zusammen 180° groß
a) Berechnen Sie für die Funktion f(x) = x2 + 2x den Funktionswert an der Stelle xo - 1
f(xo - 1) = (xo - 1)2 + 2(xo - 1) = =
b) Berechnen Sie den Wert der Terme: (1,25·105)/(5·10-3)
c) Lösen Sie die folgende Gleichung: |x - 3| < 2 Fallunterscheidung:
für x > 3 folgt: x - 3 < 2 x1
für x < 3 folgt: -(x - 3) < 2 x2 =
Ergebnis: Lösung sind alle die Zahlen, die von 3 einen kleineren Abstand als 2 haben !!!
d) Stellen Sie die Gleichung: u = (m1·v1+ m2·v2)/(m1+ m2) nach v2 um!
e) Benennen und erläutern Sie den Höhensatz (aus der Satzgruppe des Pythagoras) an einer geeigneten Skizze!
Tägliche Übungen - Mathematik Klasse 12-I GK
Tägliche Übungen - Mathematik Klasse 12-II GK
a)
Tägliche Übungen - Mathematik Klasse 13-I GK
Tägliche Übungen - Mathematik Klasse 13-II GK