Übungen - Physik   Klasse 11-I GK

          Übung: Einführung in die Kinematik

1.     Ein LKW fährt um 12 Uhr von Frankfurt nach München (Entfernung ca. 500 km). Seine mittlere Geschwindigkeit beträgt 60 km/h. Ein halbe Stunde später startet ein PKW von Frankfurt mit einer mittleren Geschwindigkeit von 100 km/h. 

  1.      Wo und wann wird der LKW vom PKW überholt? 

  2.      Wo und wann begegnen beide Fahrzeuge einem Motorradfahrer, der um 13 Uhr von München in die umgekehrte Richtung gestartet ist, und mit einer mittleren Geschwindigkeit von 80 km/h fährt? (Hinweis: Fertigen Sie ein geeignetes Diagramm an, in dem die Bewegung der drei Körper zeitgleich dargestellt wird!)

       

LKW:   s = 60·t        Auto:   s = 100·t - 50        Motorrad:   s = -80·t + 580

LKW/Auto:  60·t = 100·t - 50    40·t = 50    t = 5/4(h)        s = 60·5/4 = 75(km) = 100·5/4 - 50

LKW/Motorrad: 60·t = -80·t + 580   140·t = 580   t = 4,14(h)   s = 60·4,14 = 248,57(km) = -80·4,14 + 580

Auto/Motorrad:  100·t-50 =-80·t+580   180·t = 630    t = 3,5(h)    s = 100·3,5-50 = 300(km) = -80·3,5+580

2. Bei einem Autorennen schafft ein Wagen in der ersten Runde nur eine durchschnittliche Geschwindigkeit von 100 km/h. Der Fahrer möchte aufholen und über die ersten beiden Runden eine Durchschnittsgeschwindigkeit von 200 km/h einhalten. Kann er das schaffen? Mit welcher Geschwindigkeit müsste er dann in der zweiten Runde fahren? (Hinweis: Geben Sie sich zunächst eine konkrete Streckenlänge für eine Runde vor, und verallgemeinern Sie dann Ihr Ergebnis!)

             

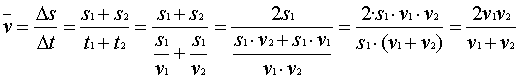
        v·(v1+v2) = 2·v1·v2       v·v1+v·v2 = 2·v1·v2        v·v1 = 2·v1·v2 - v·v2         v·v1 = (2·v1 - v)·v2       v2 =  v·v1/(2·v1 - v)·  

            Nenner des Bruches wird Null, wenn v = 2·v1

                home                     Stoff                                zurück                        HA                               top

        Übung: Augenblicks- und Durchschnittsgeschwindigkeit

Aufgabe:

Ein PKW legt auf einer Landstraße in 1,5 Stunden 70 km zurück. Danach legt er eine halbstündige Pause ein. Im Anschluss fährt er eine halbe Stunde mit einer Geschwindigkeit von 140 km/h auf der Autobahn. Zum Schluss folgt eine einstündige Ortsdurchfahrt mit 40 km/h. Alle Bewegungsabschnitte sollen annähernd gleichförmig ablaufen. 

  1. Zeichnen Sie ein s-t-Diagramm der Gesamtbewegung!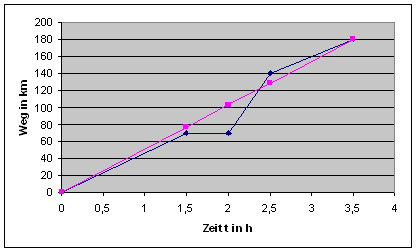 

  2. Berechnen Sie die Durchschnittsgeschwindigkeit der Gesamtbewegung!      v = 51,4 km/h

  3. Zeichnen Sie in ihr s-t-Diagramm einen weiteren Graphen, der über den gesamten Zeitraum eine gleichförmige Bewegung mit dieser Geschwindigkeit darstellt! 

  4. Vergleichen Sie die Geschwindigkeiten im I. und  IV. Bewegungsabschnitt, ohne die Geschwindigkeit in Bewegungsabschnitt I  auszurechnen!                                           Anstieg des Geradenstückes I ist größer als der des Geradenstückes IV, also ist auch vI größer als vIV  ( 46,67 km/h > 40 km/h)

          home                     Stoff                                zurück                        HA                               top

        Übung: Geradlinig gleichförmige Bewegung

Aufgabe:

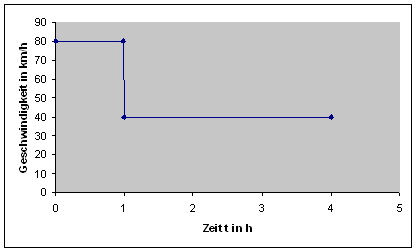
Ein Fahrzeug bewegt sich gleichförmig und legt in 4 Stunden einen Gesamtweg von 200 km zurück. Dabei fährt es  auf dem ersten Teilstück s1 mit 80 km/h und auf dem zweiten Teilstück s2 mit 40 km/h.

Berechnen Sie die Länge der beiden Teilstücke s1 und s2!

geg.: v1 = 80 km/h                                                             ges.: s1, s2

        v2 = 40 km/h

         s = 200 km

         t = 4 h

Lösung:  s = s1 + s2                  t = t1 + t2          s = v·t

             s = v1·t1 + v2·t2           t2 = t - t1

             s = v1·t1 + v2·(t - t1)

             s = v1·t1 + v2·t - v2·t1 /-v2·t

             s - v2·t = (v1 - v2)·t1     

               t1 = (s - v2·t)/(v1 - v2) = (200km - 40km/h·4h)/(80km/h - 40km/h)

            t1 = 1 h        t2 = t - t1 = 4h - 1h = 3h  

            s1 = 80km/h·1h = 80 km          s2 = 200km - 80km = 120 km

          home                     Stoff                                zurück                        HA                               top

        Übung: Gleichmäßig beschleunigte Bewegung

Aufgabe:

Die Startbahn für Flugzeuge auf einem Flugzeugträger ist 278 m lang. Das Flugzeug hebt mit einer Geschwindigkeit von 495 m/s ab. 

Wie groß ist die als konstant angesehene Beschleunigung?

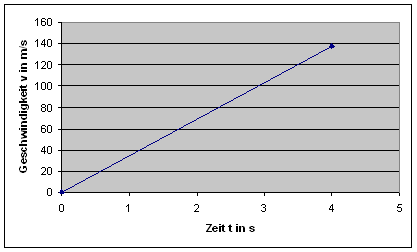geg.: v = 495 km/h = 137,5 m/s                            ges.: a

         s = 278 m

Lösung:    s = ½a · t2           v = a · t

                                          t = v/a

               s = ½a · (v/a)2 = ½a · (v2/a2) = ½·v2/a   /·2a

          2·a·s = v2

             a = v2/(2s) = (137,5m/s)2/(2·278m) = 34 m/s2

Eine Rakete, die mit a = 45 m/s2 beschleunigt wird, hat die Geschwindigkeit  v = 900 m/s  erreicht. Welchen Weg legt sie in den nächsten 2,5 Sekunden zurück?

Ein LKW verringert durch gleichmäßiges Bremsen seine Geschwindigkeit von 54 km/h auf 36 km/h  und legt dabei 500 m Weg zurück. Wie lange dauert der Bremsvorgang?

Ein Rennschlitten steigert beim Durchfahren einer Strecke von  125 m  in einem Eiskanal seine Geschwindigkeit von 15 m/s  auf  28 m/s. Wie groß sind die zum Durchfahren der Strecke erforderliche Zeit und die Beschleunigung?

          home                     Stoff                                zurück                        HA                               top

        Übung: Verbundene Bewegungen

Aufgabe:

Gegeben ist das v-t-Diagramm der Bewegung einer Straßenbahn.
  1. Berechnen Sie die Beschleunigung in den Bewegungsabschnitten I und III und zeichnen Sie das a-t-Diagramm!  (aI = 2m/s2   aIII = -5m/s2)
  2. Berechnen Sie den zurückgelegten Weg nach 2,5s , nach 11s und nach 14s! Berechnen Sie nun den zurückgelegten Weg nach 2s und nach 13s und skizzieren Sie das zugehörige s-t-Diagramm! 

mit sI = ½aI·tI2 + vo·tI = 1m/s2·(2,5s)2 + 10m/s·2,5s = 31,25m

  sII = vII·tII + sI = 15m/s · 8,5s + 31,25m = 158,75m

  sIII = ½aIII·tIII2+vII·tIII+sII=-2,5m/s2·(3s)2+15m/s·3s+158,75m

  sIII = 181,25m        

  s(2s) = 24m       

  s(13s) = 178,75m

          home                     Stoff                                zurück                        HA                               top

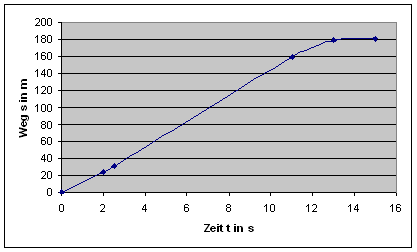
        Übung: Der freie Fall

1a)  Mit welcher Geschwindigkeit trifft ein Springer auf die Wasseroberfläche, der vom 5–m– Brett springt? Geben sie die Geschwindigkeit in m/s und in km/h an!   9,9m/s = 35,66 km/h

  1. Um welchen Faktor vergrößert sich die Auftreffgeschwindigkeit, wenn vom  10 – m – Turm gesprungen wird?        um  k = ½·√2  auf 14,0 m/s

  2. Aus welcher Höhe müsste er springen, um eine doppelt so große Endgeschwindigkeit zu erreichen?                  aus 20 m Höhe

  1. Ein PKW fährt mit einer Geschwindigkeit von 50 km/h gegen eine Mauer. Aus welcher Höhe müsste das Auto frei gefallen sein, um ebenfalls mit 50 km/h am Boden aufzutreffen?   aus 9,83 m Höhe

  1. Der Brunnen einer hohen Burg hat bis zum Wasserspiegel eine Tiefe von  126 m . Welche Zeit vergeht, bis man den Aufschlag eines Steines hört, der vom Rande des Brunnens herunterfällt?  t = 5,07s + 0,38s = 5,45s

          home                     Stoff                                zurück                        HA                               top

        Übung: Überlagerte Bewegungen - das Unabhängigkeitsprinzip

Die Bewegung eines Pakets soll in einem zweidimensionalen kartesischen Koordinatensystem (1 Einheit = 1m) beschrieben werden. Dieses Paket soll mit Hilfe eines automatisierten Gabelstaplers vom Punkt  P1(4/12)  zum Punkt  P2(10/2)  bewegt werden.

  1. Mit welcher Geschwindigkeit muss Motor 1 den Gabelstapler horizontal und Motor 2 den Gabelstapler gleichzeitig vertikal bewegen, damit die Bewegung nach  4 s  beendet ist?  vx = ∆x/∆t = 6m/4s = 1,5 m/s                        vy = ∆y/∆t = -10m/4s = -2,5m/s

  2. Wie weit hat sich das Paket bewegt?   P1P2 = √(10m-4m)2+(2m-12m)2 = √(36m2 + 100m2) = 11,66m

  3. Welche resultierende Geschwindigkeit hat das Paket während der Bewegung?  v =∆s/∆t =11,66m/4s =2,92m/s   oder  v =√(vx2 + vy2) =√(1,5m/s)2 + (-2,5m/s)2) = 2,92m/s

  4. Welche Neigung hat die „Bahnkurve“ des Pakets gegenüber der Horizontalen?  tanα = vy/vx = -2,5/1,5 = 1,67  daraus folgt α = -59°   oder  α = 121°

          home                     Stoff                                zurück                        HA                               top

        Übung: Der senkrechte Wurf

  1. Ein Stein wird mit einer Anfangsgeschwindigkeit  voy = 16 m/s  senkrecht in die Höhe geworfen.

    a) Wie groß sind die Steigzeit und die Steighöhe?   th = 1,63 s  sh = 13,05 m                                                                                                                                  

     b) Welche Zeit vergeht bis zum Aufschlag auf den Boden, der  2 m  unter der abwerfenden Hand liegt?                                                                                                               0 = -4,905·t2 + 16·t + 2    0 = t2 - 3,26·t - 0,41    t1/2 = 1,63 ± √3,067    t1 = 3,38s    (t2 = -0,12s entfällt)

     

  2. Ein Stein wird mit einer Anfangsgeschwindigkeit von  20 m/s  senkrecht nach unten geworfen. Nach 22 m prallt er auf.  Um wie viel  m/s  ist er schneller als ein gleichartiger Stein, der aus derselben Höhe frei fällt?                freier Fall: t = √2y/(-g) = 2,12s    vy = -g·t = -20,8 m/s        oder        v = √(2y·g) = 20,8 m/s             senkrechter Wurf nach unten: aus 0 = -4,905t2 - 20t + 22    folgt  t1 = 0,90 s   und  vy = -g·t - voy = -28,83m/s

 

  1. Ein senkrecht empor geworfener Körper hat in einer Höhe von 20 m die Geschwindigkeit 8 m·s-1. Zu berechnen sind die Anfangsgeschwindigkeit vo und die Flugzeit tF bis zur Rückkehr zum Startpunkt!  mit Hilfe eines Gleichungssystems erhält man:  vo = 21,36m/s  tF = 4,36s

         home                     Stoff                                zurück                        HA                               top

        Übung: Der waagerechte Wurf

Aufgabe:

Eine Kugel rollt von einem kleinen Tischchen mit einer waagerechten Geschwindigkeit von 2,45 m/s und schlägt nach 0,19s auf der Unterlage auf.

  1. Berechnen Sie die Höhe des Tischchens!   yo = 0,18m

  2. Berechnen Sie die horizontale Entfernung des Aufschlagpunktes von der Tischkante!  xW = 0,47m

  3. Berechnen Sie die Aufschlagsgeschwindigkeit!   v = 3,1 m/s

Aufgabe:

Um die Abwurfgeschwindigkeit vo eines Wurfgerätes zu bestimmen, richtet jemand das Gerät waagerecht aus und lässt es eine Kugel abschießen, die in einem horizontalen Abstand von 4,25 m auf dem 1,12 m tiefer liegenden Fußboden aufschlägt. 

  1. Wie groß war die Abschussgeschwindigkeit?   vox = 8,9 m/s
  2. Wie groß ist die Aufschlagsgeschwindigkeit?   v = 10,1 m/s
  3. Unter welchem Winkel zur Horizontalen trifft die Kugel auf den Fußboden?  α = 27,9°

          home                     Stoff                                zurück                        HA                               top

        Übung: Der schräge Wurf

Aufgabe:

Aus einer Luftpistole wird in Erbodenhöhe ein Geschoss unter einem Winkel von 10° gegen die Horizontale mit einer Anfangsgeschwindigkeit von 80 m/s abgeschossen.

  1. Berechnen Sie die Flugweite des Geschosses!   xW = 223,1 m

  2. Berechnen Sie die Flugzeit des Geschosses!    t =  2,83 s

  3. Berechnen Sie die Geschossgeschwindigkeit v für den Zeitpunkt des Einschlages!  v = 80 m/s

          home                     Stoff                                zurück                        HA                               top

Lösungen zum Arbeitsblatt: zur Vorbereitung der Physikklausur

Thema: Mechanik

a)    Kinematik 

1.)    Ein Kradfahrer erblickt in 50 m Entfernung eine Ortstafel, von der ab er nur mit einer   Geschwindigkeit  v2 = 50 km/h  fahren darf. Wie lange dauert der Bremsvorgang und wie groß ist die Bremsverzögerung, wenn seine Anfangsgeschwindigkeit  v1 = 80 km/h beträgt?           

geg.:     vo = 80 km/h = 22,22 m/s            ges.: t, a (gleichmäßig beschleunigte Bewegung mit AB)

            v  = 50 km/h = 13,89 m/s

            s  = 50 m

Lösung: v = √(2as + vo2)   umstellen nach a       s = ½(v+vo)·t   umstellen nach t

            a = (v2-vo2)/2s = -3,01 m/s²                 t = 2s/(v+vo) = 2,77s

2.)    Eine Lokomotive fährt aus dem Ruhezustand gleichm. beschleunigt an, ihre Beschleunigung beträgt a=0,6 m·s-2.

a)      Wie lange dauert es, bis Sie die Geschwindigkeit v = 80 km/h erreicht?

b)      Welche Entfernung hat sie dann vom Ausgangsort?

geg.:     v  = 80 km/h = 22,22 m/s            ges.: t, s (gleichmäßig beschleunigte Bewegung ohne AB)

            a  = 0,6 m/s2

Lösung: v = √(2as)   umstellen nach s       v = a·t   umstellen nach t

            s = v2/2a = 411 m                       t = v/a = 37,0 s

3.)    Von der US-Air-Force wurden 1954 in Neumexiko auf einer langen Schienenstrecke Beschleunigungsversuche durchgeführt, um die Belastbarkeit des Menschen für Raumfahrtprojekte zu untersuchen. Mit Hilfe von Raketentriebwerken wurden Schlitten längs einer Teilstrecke s1 = 840 m mit einer Beschleunigung a1 = 70 m·s-2 angetrieben.

Auf dem zweiten Teil der durchfahrenen Strecke von der Länge s2 = 210 m wurde der Schlitten mit Bremsschaufeln, die in ein Wasserbecken eintauchten, abgebremst.

a)      Welche Geschwindigkeit hatte der Raketenschlitten nach Durchfahren der ersten Teilstrecke?

b)      Wie lange wurde er längs dieser Strecke beschleunigt?

geg.:     a = 70 m/s2            ges.: v, t (gleichmäßig beschleunigte Bewegung ohne AB)

            s  = 840 m

Lösung: v = √(2as)                                                  s = ½·a·t2   umstellen nach t

            v = 343 m/s = 1235 km/h                             t = √(2s/a) = 4,90s

c)      Wie lange dauert der Bremsvorgang auf der zweiten Teilstrecke?

d)      Mit welcher Beschleunigung wurde der Schlitten abgebremst?

geg.:     vo = 1235 km/h = 343 m/s            ges.: t, a (gleichmäßig beschleunigte Bewegung mit AB)

            v  = 0 km/h = 0 m/s

            s  = 210 m

Lösung: v = √(2as + vo2)   umstellen nach a       s = ½(v+vo)·t   umstellen nach t

            a = (v2-vo2)/2s = -280,1 m/s²               t = 2s/(v+vo) = 1,22s

e)      Zeichnen Sie das  v-t-Diagramm!

4.)    Ein Radfahrer führt bis zum Zeitpunkt  t1 = 4,0 s  eine gleichmäßig-beschleunigte Bewegung aus. Zum Zeitpunkt  to = 0 s  durchläuft er den Ort  xo = 0 mit  einer Geschwindigkeit von  vo = 2 m·s-1 . Seine Beschleunigung beträgt  a = 1,2 m·s-2 .  Von  t1  bis       t2 = 12,0 s fährt er gleichförmig mit derjenigen Geschwindigkeit  v1 weiter, die er zum Zeitpunkt  t1  erreicht hatte. Von der Zeit  t2  an bremst er sein Rad gleichmäßig bis zum Stillstand nach  t3 = 18,0 s  ab. Dabei befindet er sich im Ort  x3 = 80,0 m.

a)      Stellen Sie die Orts-Zeit-Gleichung und die Geschwindigkeits-Zeit-Gleichung dieser Bewegung für den Zeitraum  to < t < t1 auf

x = ½·a·t2 + vo·t                                       v = a·t + vo

b)      Berechnen Sie  x1  und  v1 !

x1 = ½·1,2m/s²·(4,0s)2 + 2m/s·4,0s           v1 = 1,2m/s2·4,0s + 2m/s

x1 = 17,6 m                                             v1 = 6,8 m/s

c)      Berechnen Sie  s2 !

s2 = v1·(t2 – t1) = 6,8m/s · 8s = 54,4 m  (Beachte: x2 ist dann 17,6m + 54,4m = 72m )

d)      Zeichnen Sie das  x-t-Diagramm und das  v-t-Diagramm dieser Bewegung für den Zeitraum  to <  t  <  20 s !

5.)    Eine eiserne Schraube fällt von einem Werftkran aus einer Höhe von  65 m  zu Boden.

Nach welcher Zeit und mit welcher Geschwindigkeit trifft sie auf dem Boden auf?

geg.:     s  = 65 m                         ges.: t, v (gleichmäßig beschleunigte Bewegung ohne AB)

            g  = 9,81 m/s2                                            (freier Fall)

Lösung: v = √(2gs)                                          s = ½·g·t2   umstellen nach t

            v = √(2·9,81m/s2·65m)                         t =  √(2s/g) = √((2·65m)/9,81m/s2)

    v = 35,7 m/s                                        t = 3,64 s

6.)    Bei einem Ausbruch des Vesuv wurde beobachtet, dass einzelne Steine bis zu einer Höhe von  2 km  hoch geschleudert wurden. Ermitteln Sie die Mindestgeschwindigkeit  vo, mit der die Steine senkrecht aus dem Krater geschleudert wurden:

geg.:     sh  = 2000 m                                    ges.: vo (senkrechter Wurf nach oben)

            g  = 9,81 m/s2                                           

Lösung: sh = vo2/(2g)  nach vo umstellen                                           

            vo = √(2·g·sh) = √(2·9,81m/s2·2000m)            

    vo = 198,1 m/s                                        

7.)    Von einem  40 m  hohen Holzturm wirft ein Krieger einen Speer in horizontaler Richtung mit einer Anfangsgeschwindigkeit von  20 m·s-1. In welcher horizontalen Entfernung vom Fußpunkt des Turmes und mit welcher Geschwindigkeit kommt der Speer auf dem Boden auf? Unter welchem Winkel steckt er im Boden?

geg.: yo  = 40 m                                            ges.: xw, v, α (waagerechter Wurf )

        vox = 20 m/s

g  = 9,81 m/s2                                           

Lösung: erst Fallzeit ermitteln: s = ½·g·t2   umstellen nach t                               

                                            t =  √(2s/g) = √((2·40m)/9,81m/s2) = 2,86 s

       dann in x-Richtung:  x = vox·t = 20m/s · 2,86s = 57,1 m

Gesamtgeschwindigkeit setzt sich aus vx und Fallgeschwindigkeit vy zusammen:

                                      vx = 20m/s = vox    vy = -g·t = -9,81m/s2·2,86s = -28,0 m/s

                                      v = √(vx2 + vy2) = 34,42 m/s

Auftreffwinkel über rechtwinkliges Geschwindigkeitsdreieck:

                                      tan α = vy/vx = (-28,0m/s)/(20m/s) = -1,4     α = -54,5°

8.)    Ein unter einem Winkel  α = 20°  aufwärts gestelltes Förderband wirft Bauschutt mit einer Anfangsgeschwindigkeit von  2,2 m·s-1  in eine  4 m  unter seinem oberen Ende stehende Lore. Wie groß ist die Wurfweite?

             

       Übung: Einführung in die Dynamik

Aufgabe:

          home                     Stoff                                zurück                        HA                               top

        Übung: Die physikalische Größe Kraft

Aufgabe:

          home                     Stoff                                zurück                        HA                               top

        Übung: Kräfteaddition, Kräftezerlegung

Aufgabe:

          home                     Stoff                                zurück                        HA                               top

       

         Übung: Newton'sche Axiome

  1. Ein Kleinwagen ( m = 750 kg Leergewicht ) beschleunigt in 25 s aus dem Stillstand auf 100 km/h, wenn man ihn voll ausfährt. Die Masse des Fahrers betrage 50 kg. Nun steigen vier weitere Personen mit einer Gesamtmasse von 200 kg ein.   Wie lange dauert es nun, bis 100 km/h erreicht werden?

  2. Ein Pkw beschleunigt in 8,5 s von Null auf 100 km/h. Welche Antriebskraft ist dafür nötig, wenn die Masse des Fahrzeuges 950 kg beträgt?

  3. Ein Ball (m =0,5 kg) wird 10 m  hochgeworfen. In 0,1 s erreicht er die dafür erforderliche Geschwindigkeit.  Wie groß ist die dafür erforderliche Kraft? (Gehen Sie von einer glm. beschleunigten Bewegung beim Abwurf des Balles aus!)   

  4. Ein Radfahrer fährt mit einer Geschwindigkeit von 20 km/h. Die Masse von Fahrer und Rad beträgt zusammen  80 kg. Er rollt ohne weiteren Antrieb aus und kommt nach 50 m zum Stehen.  Wie groß ist die Reibungskraft, wenn man annimmt, dass er gleichmäßig abgebremst wird

  5. Ein PKW ( m = 950 kg ) fährt mit 50 km/h frontal auf eine Wand. Seine Frontpartie wird dabei um 70 cm verkürzt.      Wie groß ist die mittlere Bremsbeschleunigung und die mittlere Bremskraft bei diesem Vorgang?

  6. Am Kranseil eines Turmdrehkrans hängt eine Betonplatte der Masse 2,5 t. Wie groß ist die Kraft im Seil,  wenn die Platte:

bullet

a.    mit der konstanten Beschleunigung von 1,2 m·s-2 gehoben

bullet

b.    mit konstanter Geschwindigkeit gehoben wird    oder

bullet

c.     in Ruhe hängt?

  1.  Eine Kiste steht auf einer geneigten Ebene mit einem Neigungswinkel von 5° . Wie groß muss die Reibungszahl mindestens sein, damit die Kiste nicht rutscht?

  2. Ein Quader mit der Gewichtskraft FG soll auf einer um den Winkel α geneigten Ebene gleichförmig nach   oben geschoben werden.  Welche Kraft muss an dem Quader angreifen, wenn die Reibungszahl μ beträgt?

            home                     Stoff                                zurück                        HA                               top

       

         Übung: Spezielle Kräfte und Prinzip von d'Alambert

            home                     Stoff                                zurück                        HA                               top

Übungen - Physik   Klasse 11-II GK

     Übung: Arbeit und Energie

Aufgabe:  Ein Körper der Masse 13 kg soll von einem Gerüst (2,50 m über dem Erdboden) auf das Dach eines Hauses (8,50 m) gehoben werden.

    a) Welche Hubarbeit ist dafür notwendig?    WHub = m·g·h1 = 13kg·9,81m/s2·6m = 765,18 J

    b) Welche potentielle Energie hat der Körper auf dem Dach gegenüber dem Gerüst?  Epot = WHub = 765,18J

    c) Welche potentielle Energie hat der Körper auf dem Dach gegenüber dem Boden?          Epot2 = WHub2 = m·g·h2 = 13kg·9,81m/s2·8,50m = 1084 J

Aufgabe:  

4. Ein Fahrzeug mit 40 km/h erzeugt bei blockierten Bremsen eine Bremsspur von 10 m Länge. Wie lang ist seine Bremsspur bei 160 km/h? Hängt die Länge der Bremsspur von der Masse des PKW ab?

WR = ∆Ekin   μ·m·g·s = 0,5·m·v2     s = v2/(2·μ·g)     s ~ v2 ( μ = konst.)    aus v2 = 4·v1 folgt s2 = 16·s1 = 160 m

5. Eine Skiläuferin (m = 50 kg) fährt einen 40 m langen Abhang mit einem Neigungswinkel von 40° hinab. Welche Geschwindigkeit und welche kinetische Energie erreicht sie am Ende des Abhanges, wenn:                    a) die Bewegung als völlig reibungsfrei angenommen wird  EkinE= EpotA= m·g·h =m·g·l·sinα =12,6 kJ (22,5 m/s) b) die Reibung mit einer Gleitreibungszahl von 0,1 berücksichtigt wird? 

EkinE2 = EpotA - WR = m·g·l·sinα - μ·m·g·cosα·l = m·g·l·(sinα - μ·cosα) = 11,1 kJ      v = √(2·Ekin)/m = 21.1 m/s)

Wie groß ist die zur Überwindung der Reibung erforderliche Arbeit bei Aufgabe b?  WR = ∆Ekin = 1,5 kJ

            home                     Stoff                                zurück                        HA                               top

Aufgabe:  Ein Pflug wird von einem Traktor mit einer Kraft von 32 kN 6,3 km durch ein Feld gezogen. Dabei wirkt die Gegenkraft des Pfluges unter einem Winkel von 15° gegenüber der Horizontalen. Wie groß ist die vom Traktor am Pflug verrichtete Arbeit?

           W = Fs· s = F · cosα · s  

          W =  32000N·cos15°·6300m 

          W = 1,95·108 J  =  195 MJ

6. Eine Armbrust kann einen Pfeil (m = 100 g) hundert Meter hoch schießen. Der Spannweg beträgt 10 cm. Mit welcher Maximalkraft muss die Armbrust gespannt werden?

Epot(V) = Epot(L)        0,5·Fmax·s = m·g·h            Fmax = (2·m·g·h)/s  =  1962 N

            home                     Stoff                                zurück                        HA                               top

         Übung: Arbeit und Energie (II)

1. Zum Spannen eines Bogens sei eine Kraft von 200 N erforderlich, um die Sehne mit dem Pfeil um 30 cm zurück zu ziehen. Mit welcher Geschwindigkeit verlässt der 75 g schwere Pfeil den Bogen, wenn ein linearer Zusammenhang zwischen Spannkraft und Spannweg angenommen werden darf?

0,5·Fmax·s = 0,5·m·v2        v = √(F·s)/m  =  28,3 m/s

2. Ein Skispringer der Masse 72 kg geht nach Verlassen des Balkens mit einer Anfangsgeschwindigkeit von 2,5 m/s in die Spur. Die Spurlänge beträgt 45 m. Mit welcher Geschwindigkeit verlässt er den 30 m tiefer gelegenen Schanzentisch, wenn man die Schanze als geneigte Ebene ansieht und:

bulletReibung vernachlässigt wird    EpotL + Ekin1 = Ekin2        v2 = √(2·g·h + v12)  =  24,4 m/s
bulleteine Gleitreibungszahl von 0,02 und ein mittlerer Luftwiderstand von 80 N angenommen wird?

EpotL + Ekin1 = Ekin2 + WR        mgh + 0,5mv12 = 0,5mv22 + μ·cosα·mgs + FL·s        v2 = 21,9 m/s

3. Wie hoch springt eine Kugel von 100 g  Masse, die auf eine um x = 20 cm zusammengedrückte Feder mit einer Federkonstante von D = 1,5 N/cm gelegt wird, wenn sich diese plötzlich entspannt?

0,5·D·s2 = m·g·(h + s)        h = 2,86 m über dem Ende der entspannten Feder

5. Ein Körper von 12 kg Masse fällt aus einer Höhe von 70 cm auf eine gefederte Unterlage mit D = 40 N·cm-1 . Um welches Stück s wird die Feder dabei maximal zusammengedrückt?

mg(h + s) = 0,5Ds2        quadr.Gleichung:  s2 - 0,059s - 0,041 = 0        s1 = 0,2345 m    s2 < 0 entfällt

6. Ein Körper der Masse 60 g fällt aus 0,5 m  Höhe auf eine senkrecht stehende, entspannte Schraubenfeder   (D = 750 N/M). 

bullet Um welche Länge x wird die Feder zusammengedrückt, und welche Arbeit wird reibungsfreien Ablauf des Vorganges an der Feder verrichtet? wie 5.    s2 - 0,00157s - 0,000785 = 0      s1 = 0,02881 m    WV= 0,31 J
bullet Auf welche Höhe über dem freien Ende der entspannten Feder steigt der Körper,  wenn bei der Entspannung der Feder 5 % der Gesamtenergie durch Reibung in thermische Energie umgewandelt wird? 

0,95·0,5·D·s12 = m·g·(h + s)       h = (0,475·D·s12)/(m·g) - s        h = 47,3 cm

bullet Mit welcher Startgeschwindigkeit muss die Kugel aus der gleichen Höhe wie bei Aufgabe a) nach unten geworfen werden, wenn die Feder um 3,2 cm zusammengedrückt werden soll?

m·g·(h + s)  + 0,5·m·vA2 =  0,5·D·s2        vA = √(D·s2 - 2·m·g·(h + s))/m  =  1,54 m/s

7. Ein Fadenpendel der Länge 1m wird aus seiner vertikalen Gleichgewichtlage um 60° ausgelenkt. 

bullet Berechnen Sie die Geschwindigkeit des Pendelkörpers beim Durchgang durch die Ruhelage (Gleichgewichtslage)!     m·g·l·(1-cosα) = 0,5·m·v2        v = √(2·g·l·(1-cosα))  =  3,13 m/s
bullet Beim Erreichen der Gleichgewichtslage wird das Pendel durch einen Stift S auf eine Länge von 40cm verkürzt (Hemmungspendel). Welche Geschwindigkeit hat der Pendelkörper beim Durchgang durch die Horizontale zum Stift S?    m·g·l·(1-cosα) = m·g·h* + 0,5·m·v2        mit h* = 0,4 m   folgt   v = 1,4 m/s

            home                    Stoff                               zurück                        HA                               top

        Übung: mechanische Leistung

1. Welche Leistung kann ein aus 0,8 m Höhe frei herabfallender Schmiedehammer von 15 kg Masse beim Auftreffen auf den Amboss abgeben? In welcher Form tut er das?

P  =  F · v  =  m·g·v  =  m·g·√(2·g·h)  =  583 J        Verformung, Erwärmung

            home                    Stoff                               zurück                        HA                               top

         Übung: Kraftstoß und Impuls

  1. Auf eine ruhende Rakete von 3,5 t Masse wirkt für 4 s eine Schubkraft von 1,2·105 N. Berechnen Sie den Kraftstoß, die Impulsänderung und die erreichte Endgeschwindigkeit!  S = 4,8·105Ns = ∆p  vE = 137,1 m/s
  2.  
  3.  
  4.  
  5.  
  6.  
  7.  

            home                    Stoff                               zurück                        HA                               top

        Übung: elastischer Stoß

Aufgabe:  Eine Kugel 1 mit der Masse m1 = 200 g stößt mit einer Geschwindigkeit von 15 cm/s auf eine ihr mit gleicher Geschwindigkeit entgegenkommende Kugel 2 mit der Masse m2 = 150 g. Berechnen Sie die Geschwindigkeiten beider Kugeln nach dem elastischen Zusammenstoß!

u1 = (50g)/(350g)·15cm/s + (300g)/(350g)·(-15cm/s) = -10,7 cm/s

u2 = (-50g)/(350g)·(-15cm/s) + (400g)/(350g)·(15cm/s) = 19,3 cm/s

Ergebnis:  beide Kugel kehren ihre Bewegungsrichtung um; die leichtere ist schneller; die schwere  langsamer

 

            home                    Stoff                               zurück                        HA                               top

        Übung: unelastischer Stoß

6. Ein Fahrzeug mit 750 kg Masse fährt auf ein haltendes Fahrzeug doppelter Masse. Aus dem nach dem Aufprall zurückgelegten Bremsweg wird die Geschwindigkeit  unmittelbar nach dem Stoß mit 20 km/h ermittelt. Mit welcher Geschwindigkeit fuhr das Fahrzeug 1 auf?

v1 = [(m1 + m2)·u - m2v2]/m1  =  60 km/h

Aufgabe:  Ein Mittelklassewagen mit der Masse m1 = 1500 kg stößt bei einer Geschwindigkeit von 150 km/h mit einem Kleinwagen der Masse m2 = 800 kg ,der selbst mit 80 km/h unterwegs ist, zusammen. Berechnen Sie die Geschwindigkeit der Autos nach dem unelastischen Zusammenstoß! Diskutieren Sie dabei sowohl den Auffahr- wie den Frontalunfall und untersuchen Sie durch Tausch auch den Einfluss de beiden Geschwindigkeiten!

geg.:   m1 = 1500 kg

           m2 = 800 kg

            v1 = 150 km/h

            v2 = 80 km/h

 geg.:   m1 = 1500 kg

           m2 = 800 kg

            v1 = 80 km/h

            v2 = 150 km/h

 geg.:   m1 = 1500 kg

           m2 = 800 kg

            v1 = 150 km/h

            v2 = -80 km/h

 geg.:   m1 = 1500 kg

           m2 = 800 kg

            v1 = 80 km/h

            v2 = -150 km/h
ges.:   u ges.:   u ges.:   u ges.:   u
Lösung:  

u=(m1v1+m2v2)/(m1+m2)

u = 125,65 km/h

 Lösung:  

u=(m1v1+m2v2)/(m1+m2)

u = 104,35 km/h

 Lösung:  

u=(m1v1+m2v2)/(m1+m2)

u = -70 km/h

 Lösung:  

u=(m1v1+m2v2)/(m1+m2)

u = 0 km/h

Ergebnis:  das leichtere Fahrzeug erfährt grundsätzlich die deutlich höhere Geschwindigkeitsänderung, d.h. die Insassen des leichteren Fahrzeuges erfahren die deutlich größeren Beschleunigungen und sind damit dem größeren Verletzungsrisiko ausgesetzt

3.  Beim Zerfall eines Radiumkerns wird ein Alphateilchen mit der Geschwindigkeit 1,5·107 m/s emittiert. Welchen Impuls und welche Geschwindigkeit erhält der Tochterkern bei diesem Vorgang?

Zerfallsgleichung:   also:    u2 = - (4/222) ·1,5·107m/s = 2,7·105m/s

            home                    Stoff                               zurück                        HA                               top

        Übung: gleichförmige Kreisbewegung

  1. Die Erde bewegt sich mit einem Abstand von einer astronomischen Einheit (1 AE  =  1,49 · 1011 m) nahezu auf einer Kreisbahn um die Sonne. Berechnen Sie die Bahngeschwindigkeit (in km/s) sowie die Winkelgeschwindigkeit der Erdbewegung!  v = 29,7 km/s   ω = 0,0172 d-1 = 0,000 000 199 s-1

  2. Berechnen Sie die Bahngeschwindigkeit sowie die Winkelgeschwindigkeit für einen Punkt auf der Erdoberfläche aufgrund der Erdrotation um ihre eigene Achse! Warum bemerken wir nichts von dieser großen Geschwindigkeit?   v = 463,3 m/s = 1668 km/h     ω = 0,000 073 s-1

  3. Ein PKW soll eine nicht überhöhte Straßenkurve (Kurvenradius r = 30 m) mit v = 50 km/h  durchfahren. Geht das bei trockener Fahrbahn (Haftreibungszahl μo = 0,65) und auch bei nasser Fahrbahn (μo = 0,40) aus physikalischer Sicht gut? Was passiert, wenn beim Durchfahren der Kurve gebremst oder beschleunigt wird?  Fr = mv2/r = μ·m·g = FR         μ = v2/(r·g) = 0,655

            home                    Stoff                               zurück                        HA                               top

        Übung: Drehbewegung - gleichförmige und gleichmäßig beschleunigte Rotation

  1. Die Drehzahl einer Schleifscheibe wird innerhalb von  t = 10 s  von  3000 Umdrehungen pro Minute auf  2000 Umdrehungen pro Minute abgebremst. Wie viele Umdrehungen führt die Schleifscheibe dabei aus?  ω1 = 314 s-1       ω2 = 209 s-1       α = -10,5 s-2       φ = 2618       N = 416,67

  2. Ein Schwungrad hat die Drehzahl  n1 = 500 min-1  und wird mit der Winkelbeschleunigung  α = 5 s-2  15 Sekunden lang beschleunigt. Welche Drehzahl n2 wird dabei erreicht?  n2 = 20,27 s-1 = 1216 min-1

  4. Innerhalb von 5 Sekunden führt ein Rad 120 Umdrehungen aus und verdoppelt dabei seine Winkelge- schwindigkeit ω. Wie groß ist diese am Beginn und am Ende des Vorganges? ωo=100,53 s-1 ω1=200,06 s-1

            home                    Stoff                               zurück                        HA                               top

        Übung: Dynamik der Rotation

  1. Welchen Durchmesser d hat eine Kreisscheibe der Masse  m = 8 kg , deren Trägheitsmoment  J = 1,69 kgm² beträgt?   r = 0,65 m     d = 1,3 m

  2. Das Trägheitsmoment eines massiven Holzzylinders mit einem Durchmesser von  d1 = 0,12 m  und der Masse  m = 6 kg  soll durch einen Bleimantel der Dichte  ρ = 11300 kg/m³  verdreifacht werden. Welche Dicke d2 muss der Bleimantel aufweisen?  r2 = 0,0614 m    ∆r = 1,4 mm

  3.  

  4. Das Chassis einer vierrädrigen Limousine hat die Masse  m1 = 300 kg  und jedes der als massive Scheiben angenommenen Räder eine Masse  m2 = 25 kg . Die beim Anfahren des Wagens zu überwindende Trägheit der Gesamtmasse soll durch einen Zuschlag erhöht werden, der das Trägheitsmoment der Räder berück- sichtigt. Wie viel Prozent der Masse sind zuzuschlagen?   Zuschlag von 12,5%

  5. Eine Walze vom Durchmesser  d = 0,10 m  hängt an zwei auf ihrem Umfang aufgewickelten Fäden und fällt aus einer Höhe von 2m. Welche Winkelgeschwindigkeit ω hat sie am Ende des Weges? Welche Zeit t wird für die Fallbewegung benötigt?    ω = 102,3 s-1    v = 5,1 m/s     t = 0,78 s

  6. Gegeben ist eine geneigte Ebene der Höhe h. Vergleichen sie die Endgeschwindigkeiten, die ein reibungs- frei heruntergleitender Körper bzw. eine herunterrollende Kugel gleicher Masse haben!  v = √(10/7·g·h)

  7.  

  8. Eine Kurve mit dem Radius von  r = 600 m soll für eine Zuggeschwindigkeit von 60 km/h so gebaut werden, das die Resultierende aus Schwerkraft (Gewichtskraft) und Fliehkraft senkrecht zum Gleis steht. Um welche Höhe h muss die äußere Schiene höher als die innere verlegt werden, wenn die Spurbreite  b = 1435 mm  beträgt?   α = 2,7°    h = 67,6 mm

zusätzliche Übungen:

  1. Auf einer Drehmaschine wird ein Werkstück mit einem Durchmesser von 210 mm bei einer Drehzahl von 630 min-1 bearbeitet. Das Gesamtträgheitsmoment der Arbeitsspindel mit Werkstück beträgt 0,60 kgm². Die Spindel wird in 3,2 s gleichmäßig bis zum Stillstand abgebremst, der Bremstrommeldurchmesser be- trägt 180 mm. Berechnen Sie für diesen Bremsvorgang die Winkelbeschleunigung und die an der Brems- trommel angreifende Kraft! Wie groß ist die beim Bremsvorgang entstehende Wärme?  α = 20,62 s-2   und dann aus  F·r = J·α   folgt F = -137,4 N     Q = ½·J·ω2 = 1306 J

  2. Auf einem Güterbahnhof läuft ein Waggon der Masse 15,0 t von einem 1,80 m hohen Ablaufberg ab. Dabei werden 92,0% der potentiellen Energie des Waggons in kinetische Energie umgewandelt. Anschließend rollt er auf horizontaler Strecke  270 m  weiter, die Reibungszahl beträgt 6,00·10-3. Danach stößt er auf einen dort haltenden zweiten Waggon der Masse 22,0 t , wobei die Kupplung einrastet. Beschreiben Sie die auftretenden Energieumwandlungen und berechnen Sie die Geschwindigkeit der beiden Waggons nach dem Ankoppeln!   Epot(A) = 264,87 kJ  Ekin(B) = 243,68 kJ   Ekin(C) = 5297 kJ    v1 = 0,84 m/s    u = 0,34 m/s

  3. Zur Bestimmung der Geschwindigkeit eines Projektils wird dieses durch zwei Scheiben geschossen, die im Abstand von 0,80 m auf einer gemeinsamen Welle mit der Drehzahl  n = 1500 min-1 rotieren. Welche Geschwindigkeit ergibt sich, wenn die beiden Durchschussstellen um 12° gegeneinander versetzt sind?       φ = 0,20944   t = 0,00133 s    v = 600 m/s

andere Übungen unter HA

            home                    Stoff                               zurück                        HA                               top

 

Übungen - Physik   Klasse 12-I GK

        Übung: Keplersche Gesetze 

Aufgabe:

Berechnen Sie die Umlaufdauer TS und die Geschwindigkeit vS eines Satelliten, der die Erde in 500 km Höhe umkreist! Benutzen Sie dabei die Tatsache, dass der Mond 384000 km von der Erde entfernt ist und diese in 27,3 Tagen umläuft!   mit 3.Keplerschen Gesetz TS  = 6,53·10-2d also rund 94 min  ; v = 7,65 km/s

          home                    Stoff                               zurück                        HA                               top

        Übung: Gravitationsgesetz

AB Nr.1a

Berechnen Sie die Gravitationskraft zwischen:

  1. Sonne und Erde!   F = 3,54·1022N

AB Nr.2a

Interpretieren Sie das Gravitationsgesetz!

bulletAngeben der physikalischen Größen, die in der Gleichung enthalten sind

o   Das Gravitationsgesetz stellt einen Zusammenhang zwischen den sich anziehenden Massen, deren Abstand zueinander und der wirkenden Gravitationskraft her.

bulletNennen der Gültigkeitsbedingungen, unter denen die Gleichung gilt

o       Das Gravitationsgesetz gilt nach momentanem Kenntnisstand universell, d.h. es ist im gesamten Universum ohne Einschränkungen gültig (Vorsicht: dunkle Materie)

bulletAngeben des jeweils zwischen zwei physikalischen Größen bestehenden Zusammenhangs unter Nennung der dabei konstant zu haltenden Größen (i.d.R. mehrere)

o       F ~ m1; m2  , wenn r = konstant

o       F ~       , wenn m1 und m2 konstant

o       r ~       , wenn F = konstant

Nennen von Beispielen für jeden Zusammenhang
bulletDie Gravitationskraft auf einen Satelliten ist bei gleichem Abstand zum Himmelskörper umso größer, je schwerer der Satellit bzw. schwerer der Himmelskörper.
bulletDie Gravitationskraft auf einen Satelliten im Gravitationsfeld eines bestimmten Himmelskörpers ist umso größer, je dichter der Satellit an dessen Oberfläche (Mittelpunkt) herankommt.
bulletEin doppelt so schwerer Satellit erfährt im Gravitationsfeld eines doppelt so schweren Himmelskörpers die gleiche Gravitationskraft, wenn er sich in doppelter Entfernung zu dessen Mittelpunkt befindet.

AB Nr.3a

Wie groß ist die Gewichtskraft eines Körpers auf dem:

  1. Mond?   FG(Mond) ≈ 1/5 · FG(Erde)

            home                    Stoff                               zurück                        HA                               top

        Übung: Schlussfolgerungen aus dem Gravitationsgesetz

AB Nr.4a

Leiten Sie die Gleichung zur Berechnung der :

  1. Parabelbahngeschwindigkeit her!   

            home                    Stoff                               zurück                        HA                               top

        Übung: Gravitationsfelder

81)                                  

           

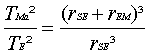
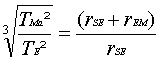
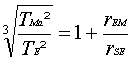
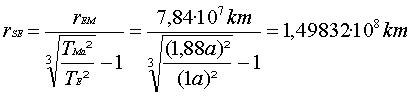
82a)   Fr = FG        mE·ω²·rSE = 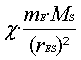             mE· ·rSE =

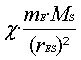
b)         MS =

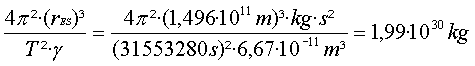
c)                     

            home                    Stoff                               zurück                        HA                               top

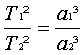
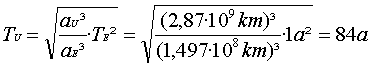
        Übung: Coulombsches Gesetz

Aufgabe:     

Vergleichen Sie die elektrische Anziehungskraft zwischen einem Proton im Atomkern und einem Elektron in der Atomhülle  mit der Anziehungskraft zwischen beiden Körpern aufgrund ihrer Massen! Nehmen Sie dazu den Atomdurchmesser mit ca. 1·10-10 m an!    FGrav = 4·10-47N    Fel = 9,2·10-8N

Hinweis: Suchen Sie sich aus dem Tafelwerk die Ruhmassen von Elektron und Proton heraus und bedenken Sie, dass beide Elementarteilchen je eine Elementarladung e tragen!

*Aufgabe:  Zwei kleine Kugeln mit gleicher elektrischer Ladung und mit gleicher Masse von je 50 mg hängen in Luft an je einem isolierenden Fädchen vernachlässigbarer Masse. Jedes Fädchen ist 60 cm lang. An ihrem gemeinsamen Aufhängungspunkt schließen beide einen Winkel von 10° ein!

a) Leiten Sie mit Hilfe einer geeigneten Skizze eine Gleichung zur Berechnung der elektrischen Ladung her!

b) Berechnen Sie den Betrag der elektrischen Ladung der Kugel!

a) Q = √16·π·εo·l2·m·g·cosα·sin3α            b)  Q = 7·10-9C

        home                        Stoff                            zurück                         HA                               top

        Übung: elektrisches Feld

        home                        Stoff                            zurück                         HA                               top

        Übung: elektrische Feldstärke

Aufgabe: Eine Kugel (r = 2,5 cm) trage eine Ladung von +9·10-12C.    Feldstärkegleichung für Punktladung

bullet

Berechnen  Sie  die  elektrische  Feldstärke  auf  der  Kugeloberfläche!    E  =  129,3 V/m

bullet

Berechnen  Sie  die  elektrische  Feldstärke  in  den  Punkte  P1  und  P2,  welche  vom  Kugelmittelpunkt    r1 = 4,5 cm  bzw. r2 = 10 cm entfernt sind!                        E1 = 38,2 V/m        E2  =  8,1 V/m

6. Im Feld zwischen zwei ungleichnamigen Ladungen ( Q1/2 = ±5·10-7C,  r = 4 cm)  befindet sich auf der Verbindungslinie  der  Mittelpunkte  der felderzeugenden Punktladungen ein Probekörper mit der Probeladung q = -3·10-9C. Er ist 3 cm von der Quelle und 1 cm von der Senke des elektrischen Feldes entfernt.

bullet

Wie groß ist die Feldstärke an dieser Stelle?    E = E1 + E2 = 4,99·106V/m + 4,49·107V/m ≈ 5·107V/m

bullet

Welche Kraft wirkt auf den Probekörper?    E = F/q         F = E·q = 0,15 N

bullet

Beschreiben Sie die aufgrund dieser Kraftwirkung ausgeführte Bewegung des Probekörpers!

im Mittelpunkt der Verbindungslinie beider felderzeugender Ladungen elektrische Feldstärke am kleinsten:    wegen E ≠ konst.  folgt F ≠ konst.  und daraus  a ≠ konst. →  geradlinig, ungleichm. beschleun. Bew. in Richtung pos. Ladung
bullet

Was passiert nach dem Zusammenstoß von felderzeugender Ladung und Probekörper?

Entladung des Probekörpers → Aufladung des Probekörpers mit entgegengesetzter Ladung → Bewegung des Probekörpers zur anderen felderzeugenden Ladung usw.

        home                        Stoff                           zurück                          HA                               top

        Übung: Spannung und Potential

1. Eine Probeladung q = 3·10-10C befindet sich 2 cm von der positiven Platte entfernt im Feld eines Plattenkon- densators mit 1 kV angelegter Spannung und einem Plattenabstand von 5 cm.

bulletBerechnen Sie die elektrische Feldstärke im Kondensatorfeld!    E = U/s = 1000V/0,05m = 20000 V/m
bulletBerechnen Sie die Feldkraft , die auf die Probeladung wirkt!       F = q·E = 3·10-10C·20000V/m = 6·10-6 N
bulletBerechnen Sie das elektrische Potential an dieser Stelle des Feldes!    φ = (U/s) ·x = 1000V/0,05m ·0,02m

                                                                                                                                 φ = 400 V  =  2/5·U,  weil x = 2/5·s

2. Eine metallische Kugel mit r = 2,5 cm trage eine Ladung von 2·10-9C.

bulletBerechnen Sie die Feldstärke im el. Radialfeld der Kugel in den Punkte P1 und P2, welche 5 cm und 10 cm vom Kugelmittelpunkt entfernt sind!                                   E1 = Q/(4πεo·r12) = 7190 V/m        E2 = 1797,5 V/m
bulletWelche Kraft wirkt im Punkt P1 auf eine positive Probeladung q = 3·10-12C?    F1 = 2,1·10-8N
bulletWelche Arbeit muss verrichtet werden, um die Ladung q im Feld der Ladung Q  von P1 nach P2 zu verschieben?                                                                                           W12 = (Q·q)/(4πεo)·(1/x1 - 1/x2) = 5,39·10-10J
bulletBestimmen Sie die Spannung zwischen den Punkte P1 und P2!    U12 = W12 /q  = 179,8 V 

        home                        Stoff                            zurück                         HA                               top

         Übung: Kondensator

  1. Gegeben sei ein Plattenkondensator mit kreisförmigen Platten vom Durchmesser 16 cm und einem Plattenabstand von s =5 mm.
    1. Welche Kapazität hat dieser Plattenkondensator?    C = 3,56·10-11 F = 35,6 pF
    2. Welche Ladung nimmt jede Platte auf, wenn eine Spannung von 1 kV angelegt wird? Q = 3,56·10-8C
    3. Bestimmen Sie die elektrische Feldstärke im Innern des Kondensators!  E = 200000 V/m
    4. Berechnen Sie die Flächenladungsdichte!    σ = 1,77·10-6 C/m2
    5. Mit welcher Kraft ziehen sich die Plattengegenseitig an?    F = E · Q = 7,12·10-3 N

    6. Bestimmen Sie die Influenzladung auf einer Metallplatte der Fläche A' = 20 cm2, die senkrecht zu den Feldlinen in das Feld gehalten werden!    q = 3,54·10-9 C

    7. Wie ändern sich die Werte für Kapazität, aufgenommene Ladung und Feldstärke, wenn statt Luft ölgetränktes Papier als Dielektrikum benutzt wird?    

    wegen C ~ εrel  folgt:    wenn εrel2 = 3·εrel1    so auch    C2 = 3·C1

    wegen Q ~ C  (aus  C = Q/U ) folgt:    wenn  C2 = 3·C1    so auch    Q2 = 3·Q1

    wegen E ~ Q und  E ~ 1/εrel    (aus   E = Q/(εo·εrel·A)  )    folgt:    E2 = E1  weil beides sich verdreifacht

  2. An einem Plattenkondensator (s = 2,7 mm) der Kapazität C = 50 nF wird eine Spannung von 300 v angelegt.
    1. Welche Ladung nimmt der Kondensator auf? Berechnen Sie die Feldstärke im homogenen Teil des Feldes!    Q = 1,5·10-5 C    E = 111111 V/m
    2. Wir verdoppeln bei angeschlossener Spannungsquelle den Plattenabstand. Wie verändern sich dann Spannung, Feldstärke und Kapazität?                                  U = konstant, also  E2 = ½·E1  und C2 = ½· C1
    3. Wir trenne den Kondensator von der Spannungsquelle und verdoppeln den Plattenabstand erneut. Welche Auswirkungen auf Spannung, Feldstärke und Kapazität treten nun ein?    nun Q = konstant, 

    also  E3 = E1 = konstant,  U3 = 2·U1 ( wegen E = U/d     gilt: U ~ d)  

                                         und C3 = ½·C1 (wegen C = ( εo·εrel·A)/d      gilt: C ~ 1/d )

        home                        Stoff                            zurück                         HA                               top

         Übung: Millikan-Versuch

Aufgabe:  In das homogene Feld eines Plattenkondensators (U = 7 kV, d = 3,5 cm) wird eine kleine Kugel mit der Masse  m = 0,1 g und der Ladung Q = 2·10-9 C eingebracht.

  1. Welche Kraft wirkt auf die Kugel, wenn die Gewichtskraft und die elektrische Feldkraft gleiche Richtungen besitzen?    F = 1,38·10-3 N    

  2. Welche Kraft wirkt auf die Kugel, wenn die Gewichtskraft und die elektrische Feldkraft entgegengesetzte Richtungen besitzen?    F = -5,81·10-4 N

  3. Die Feldstärke sei nun senkrecht zur Gewichtskraft gerichtet. Die Kugel befindet sich 1 cm von der positi- ven Platte entfernt und werde von der negativen Platte angezogen. Wo und mit welcher Geschwindigkeit trifft die Kugel auf die Platte? Welche Zeit benötigt sie dafür? Unter welchem Winkel trifft sie auf die Platte?         ax = 4 m/s2    t = 0,1118 s    vx = 0,4472 m/s   y = 0,0613 m   vy = 1,097 m/s2   vges = 1,184 m/s  die Kugel trifft 2,5 cm rechts und 6,13 cm tiefer unter einem Winkel von φ = 67,8°  mit vges auf die Platte

        home                        Stoff                            zurück                         HA                               top

        Übung: Bewegung von Elektronen im homogenen elektrischen Feld

Aufgabe:  Ein Elektron taucht mit einer Geschwindigkeit von vo = 1·106 m/s durch eine Lochöffnung in der Katode parallel zu den Feldlinien in das homogene elektrische Feld eines Plattenkondensators ein und wird in diesem beschleunigt. Mit welcher Geschwindigkeit tritt es durch die Lochöffnung an der Anode am anderen Ende des Feldes wieder aus, wenn der Kondensator eine Länge l = 5 cm und den Plattenabstand d = 3 cm aufweist und mit einer Spannung von 6 V  betrieben wird?

(Hinweis: bei dynamisch-kinetischem Lösungsweg a, t, v in dieser Reihenfolge berechnen oder über Energieerhaltungssatz probieren )

a = 3,52·1013 m/s2              t = 2,17·10-8 s (über quadratische Gleichung)               v = 1,764·106 m/s

Ekino = 4,55·10-19 J = 2,84 eV           Ekin = Ekino + e·U = 1,416·10-18 J = 8,84 eV           v = 1,764·106 m/s

Aufgabe:  Ein Elektron fliegt mit einer Geschwindigkeit von 2·106 m/s (mittig) quer zu den Feldlinien in das homogene Feld eines Plattenkondensators mit  l = 5 cm  und  d = 3 cm . In welchem Punkt und mit welcher Geschwindigkeit verlässt das Elektron das elektrische Feld, wenn die Ablenkspannung  U = 6 kV beträgt? Geben Sie die Gleichung der Geraden an, auf der es außerhalb des Feldes weiterfliegt (Koordinatenursprung im Eintrittspunkt des Elektrons)!

ay = 3,52·1013 m/s2    t = 2,5·10-8 s    y = 0,011 m    vy = 8,8·105 m/s    vges = 2,185·106 m/s     P(0,05|0,011) 

Gleichung der Parabel:  y = f(x) = 4,4 · x2                  f'(x) = 8,8·x                     f'(0,05) = 0,44= mgerade

y = 0,44x - 0,011 (über Punktrichtungsgleichung:     y - 0,011  =  0,44·(x - 0,05))

        home                        Stoff                            zurück                         HA                               top

        Übung: Magnetfeld

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Magnetische Flussdichte

Aufgabe: Das Magnetfeld eines für ein Drehspulmessinstrument verwendeten Magneten hat die magnetische Flussdichte  B = 0,0012 T. Welche Stärke I hat der durch den Kupferdraht der Drehspule fließende Strom, wenn auf ein  l = 15 mm langes Leiterstück die Kraft  F = 4,5·10-7 N wirkt?  

(Hinweis: Ersetzen Sie die Einheit  1T  durch 1N/Am)        I = F:(B·l) = 25 mA

        home                        Stoff                            zurück                         HA                               top

  Übung: Magnetfeld im Innern einer Spule

Aufgabe: Die im Experiment verwendete luftgefüllte Spule besaß 250 Windungen, hatte eine Länge von 6 cm und wurde von einer Stromstärke I = 2A durchflossen. Berechnen Sie die magnetische Flussdichte im Innern dieser Spule!    B = (1,2566·10-6VsA-1m-1·1·250·2A):(0,06m) = 0,00524 Vsm-2 = 5,24 mT

Nr.135    In einer Luftspule mit 800 Windungen, mit einer Länge von 5,0 cm und einem elektrischen Widerstand   von 45 Ω, soll ein magnetisches Feld der Flussdichte 12 mT erzeugt werden.

  1. Welche Spannung muss dafür an den Enden der Spule angelegt werden?    U = 26,86V

  2. Welche Spannung ist erforderlich, wenn sich im Innern der Spule ein Eisenkern (μrel =150) befindet? 0,18V

Nr. 133    An den Enden einer 15 cm langen Luftspule mit 850 Windungen aus 0,3 mm starkem Kupferdraht (mittlere Windungslänge 6 cm) liegt eine Spannung von 20V. Welche Flussdichte herrscht im Innern dieser Spule?    A = 0,07mm2    lD = 51m    R = 12,3Ω    I = 1,63A    B = 11,6mT

        home                        Stoff                            zurück                         HA                               top

    Übung: Lorentzkraft

Aufgabe: Ein Elektron wird in einer Elektronenstrahlröhre mit einer Spannung UB = 200V beschleunigt und in ein homogenes Magnetfeld der Flussdichte B = 1,2·10-3T eingeschossen. Dabei durchläuft es eine Kreisbahn mit dem Radius r = 4,2 cm.

  1. Berechnen Sie aus diesen Angaben die spezifische Ladung eines Elektrons und die Elektronenmasse!    e/me = 2·200V/((0,042m)2·(1,2·10-3Vsm-2)2) = 1,575·1011C/kg            me = 1,02·10-30kg

  2. Welche Geschwindigkeit hatte das Elektron bei Eintritt in das Magnetfeld?                                                           v = (e/me)·r·B = 1,575·1011C/kg·0,042m·1,2·10-3Vsm-2 = 7812000 m/s                                                             oder  v = √(2·e·U/me) = √(2·1,602·10-19As·200V/9,1·10-31kg) = 8391518 m/s

Aufgabe: Die spezifische Ladung für Protonen kann man mit folgendem Experiment bestimmen:                             Ein homogenes, vertikal gerichtetes Magnetfeld und ein homogenes, horizontal gerichtetes elektrisches Feld wirken gleichzeitig im gleichen Raumgebiet. Senkrecht zu beiden Feldlinienrichtungen treten Protonen in das Raumgebiet ein. Die magnetische Flussdichte und die elektrische Feldstärke wurden zunächst so bestimmt, dass sich die Kraftwirkungen beider Felder auf die Protonen aufheben und diese nicht abgelenkt werden. Dabei betragen die magnetische Flussdichte B = 3,9·10-3T und die elektrische Feldstärke E = 3,72·103Vm-1.

  1. Berechnen Sie daraus die Geschwindigkeit der Protonen!    v = E/B = 9,54·105 ms-1

  2. Wird dann das elektrische Feld abgeschalten, bewegen sich die Protonen auf einer Kreisbahn mit dem Radius r = 2,56m. Berechnen Sie daraus die spezifische Ladung der Protonen!                                            e/mP = v/(r·B) = 9,55·107 C/kg

        home                        Stoff                            zurück                         HA                               top

        Übung: Anwendungen der Lorentzkraft

 

        home                        Stoff                            zurück                         HA                               top

 

        Übung: Analogie zwischen den Feldern

 

        home                        Stoff                            zurück                         HA                               top

Übungen - Physik   Klasse 12-II GK

        Übung: Elektromagnetische Induktion

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Der magnetische Fluss

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Induktionsgesetz, Lenzsche Regel

  1. Wie groß ist die Induktionsspannung an den Enden einer Spule von 1500 Windungen und einer mittleren Querschnittsfläche von 9 cm², wenn sich die magnetische Flussdichte durch die Spule innerhalb einer Sekunde linear  von 0 auf 0,2 T erhöht?   Uind = (∆B·A)/∆t = (∆B·N·Ao)/∆t = (0,2T·1500·0,0009m2)/1s = 0,27V

  2. Wie groß muss die zeitliche Änderung der magnetischen Flussdichte sein, damit in einer Spule von 100 cm² Querschnittsfläche und 1000 Windungen eine Induktionsspannung von 10 V entsteht?

  1. Ein quadratischer Rahmen mit einer Seitenlänge von 8,0 cm aus Kupferdraht (5,0 cm² Querschnittsfläche) wird in 0,4 s gleichmäßig in ein homogenes Magnetfeld der magnetischen Flussdichte 0,2 T senkrecht zu den Feldlinien eingeschoben (siehe Skizze)

  1. Berechnen Sie die dabei induzierte Spannung!   Uind = (B·∆A)/∆t = (B·∆a2)∆t = (0,2T·(0,08m)2)/0,4s = 0,0032V

  2. Wie groß ist der daraufhin fließende Induktionsstrom?                                                                                 I = U/R = (U·AØ)/(ρ·l) = (0,0032V·500mm2)/(0,017Ωmm2m-1·0,32m) = 294,1A

  3. Welche Kraft muss beim Einschieben am Rahmen angreifen?   FL = I·l·B = 294,1A·0,08m·0,2T = 4,7N

  4. Berechnen Sie die beim Einschieben verrichtete Arbeit auf zwei verschiedene Arten!                                    Emech = F·s = 4,7N·0,08m = 0,376J     Eel = U·I·t = 0,0032V·294,1A·0,4s = 0,376J

  5. Wie ändert sich die Leistung beim Einschieben, wenn der Vorgang in der halben Zeit abläuft?                    wegen P = W/t = E/t also P ~ 1/t (W=E=konstant)  führt Halbierung der Einschubzeit zur Verdopplung der Leistung

  1. Im Innern einer Luftspule S1 (300 Windungen, Länge 20 cm, mittlere Windungsfläche 100 cm²)  befindet sich eine zweite Spule S2 (2000 Windungen, mittlere Windungsfläche 16 cm²).Die Spulenachsen verlaufen:

  1. parallel

  2. unter einem Winkel von 60° zueinander

  3. Welche Spannungen werden in S1 und S2 induziert, wenn sich in S1 die Stromstärke innerhalb von 8,0 ms  gleichmäßig von 4,0 A auf 1,5 A ändert? Uind2 = 1,884 V  (in Induktionsspule)    Uind1 = 1,766 V (in Erregerspule)

  1. In einem homogenen Magnetfeld der Flussdichte B = 2,8·10-2 T liegt eine kreisförmige Leiterschleife mit  d = 5,4 cm Durchmesser.

  1. Berechnen Sie den magnetischen Fluss Φ durch die Leiterschleife für den Fall, dass der Winkel φ zwischen der Flussdichte B und dem Flächenvektor A die Werte  0°, 30°, 60°, 90°, 120°, 150° und 180° annimmt!

  2. Berechnen Sie die 6 Induktionsspannungen, die bei einer konstanten Drehzahl von 3000 min-1 beim Überstreichen eines Drehwinkels von jeweils 30° entstehen!

        home                        Stoff                            zurück                         HA                               top

        Übung: Selbstinduktion, Wirbelströme

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Generator und Dynamomaschine

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Transformator

 

        home                        Stoff                            zurück                         HA                               top

 

 

Übungen - Physik   Klasse 13-I GK

        Übung: Reflexion und Brechung

Aufgabe: Berechnen Sie den Brechungswinkel β für die Stoffkombination Luft-Wasser bei einem Einfallswinkel von 50°!  

sinβ = (sinα·cwasser):cLuft = (sin50°·225000):299711         β = 35,1°   

oder          sinβ = (sinα·nVakuum-Luft):nVakuum-Wasser = (sin50°·1,000006):1,333333     β = 35,1°   

        home                        Stoff                            zurück                         HA                               top

        Übung: Totalreflexion, planparallele Platte

Aufgabe:  Berechnen Sie den Grenzwinkel der Totalreflexion für die Stoffkombination Kronglas -Wasser (Regensensor)!

sinαG/sin90° = n2/n1     sinαG = (1,333/1,51)= 0,883         αG = 62,0°       und damit viel größer als der Grenzwinkel (41,8°) für die Stoffkombination Glas-Luft (bei trockener Scheibe)

Aufgabe:  Berechnen Sie den Betrag der Parallelverschiebung des durchfallenden Lichtstrahles gegenüber dem einfallenden Strahl an einer aus leichtem Kronglas bestehenden, planparallelen Platte der Dicke  d = 5 cm , wenn der Einfallswinkel α = 45° beträgt!    

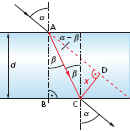        sinβ = (sinα · n1) : n2 = (sin45°·1):1,51        β = 27,9°

cosβ =  AB : AC         AC = AB : cosβ = 5cm : cos27,9° = 5,66 cm  (im Dreieck ABC)

γ =  α - β  = 45° - 27,9° = 17,1°

sinγ = CD : AC         CD = AC · sinγ = 5,66 · sin17,1° = 1,66 cm  (im Dreieck ACD)

        home                        Stoff                            zurück                         HA                               top

        Übung: Abbildung mittels Sammellinsen

Aufgabe:  Konstruieren Sie das Bild eines Gegenstandes bei Abbildung mit einer Sammellinse mit f = +30mm, wenn der Gegenstand 2cm groß ist und in 1,5cm Entfernung von der Linse aufgestellt wird!

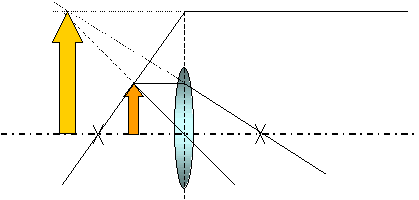
Durch Verlängerung der zunächst divergenten Strahlen auf die Gegenstandsseite der Linse erhält man im dortigen Schnittpunkt von Mittelpunkts-, Brennpunkts- und Parallelstrahl das virtuelle, vergrößerte, aufrechte Bild des Gegenstandes, so wie man es mit einer Lupe beobachten kann (jede Sammellinse kann also als Lupe benutzt werden).

        home                        Stoff                            zurück                         HA                               top

        Übung: Abbildungsgleichung für dünne Sammellinsen

Übungsblatt: Konstruktion von Abbildungen mittels Sammellinsen

gegeben gemessen gerechnet
s = 7,6cm  y = 2,5cm  f = 2,9cm s' = 4,7 cm   y' = 1,6 cm s' = 4,69 cm   y' = 1,54 cm
s = 5,7cm  y = 2,5cm  f = 2,9cm s' = 5,6 cm   y' = 2,5 cm s' = 5,90 cm   y' = 2,59 cm
s = 4,8cm  y = 2,5cm  f = 2,9cm s' = 7,3 cm   y' = 3,8 cm s' = 7,32 cm   y' = 3,81 cm
s = 1,6cm  y = 2,0cm  f = 2,9cm s' = -3,5 cm   y' = -4,2 cm s' = -3,57 cm   y' = -4,46 cm

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Abbildung mittels Spiegel und Hohlspiegel

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: optische Geräte

Aufgabe:    

        home                        Stoff                            zurück                         HA                               top

        Übung: Zusammenfassung Strahlenoptik; Abbildungs- und Sehfehler

Aufgabe:  

1.     Trifft ein Lichtstrahl unter einem Einfallswinkel von 30° auf eine planparallele Platte mit einer Dicke d = 0,5cm , so wird er bei jedem Auftreffen auf die Grenzschicht zwischen den zwei Materialien (Luft – Kronglas leicht) teilweise gebrochen und teilweise reflektiert. Berechnen Sie den Abstand der beiden reflektierten Strahlen 0. und 1.Ordnung!

           Brechungswinkel   β = 19.3° 

§        im Dreieck ΔABM gilt:                                                

       AM = BM·tan19,3° = 0,175cm     AC = 2·AM = 0,35 cm 

§        im Dreieck ΔACD gilt:                                               

      DC = AC·sin 60° = 0,303 cm

Aufgabe:  

    2.  Berechnen Sie den Grenzwinkel der Totalreflexion für die Stoffkombination Wasser – Luft!

sin αG = c1/c2 = (225000m/s)/(299711m/s)             αG = 48,65°

         oder

sin αG = n2/n1 = 1,00/1,33                                     αG = 48,75°

Aufgabe:  

3. Ein Gegenstand, der 1 cm groß ist und 7 cm von einer Linse aufgestellt wird, deren Brennweite 2 cm beträgt, soll scharf abgebildet werden. In welcher Entfernung ist der Schirm aufzustellen? Wie groß ist das Bild?

                         

        home                        Stoff                            zurück                         HA                               top

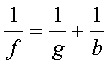
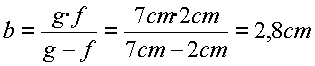
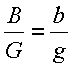
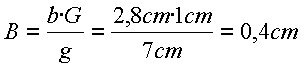
        Übung: Einführung in die Wellenoptik

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Kohärenz, Beugung und Interferenz an Doppelspalt und Gitter

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Interferenz an dünnen bzw. keilförmigen Schichten

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Polarisation und Spannungsdoppelbrechung

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Einführung in die Quantenoptik 

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Der äußere lichtelektrische Effekt (Photoeffekt)

Paetec(rot)-LB.S.469 Nr.2

aus  P = W/t = E/t = (N·h·f)/t   folgt  N = (P·t)/(h·f) = (1,7·10-18J/s·1s)/(6,626·10-34Js·5,45·1014Hz) = 4,69 also fünf

Paetec(rot)-LB.S.469 Nr.4

        WA = h·f - Ekin = h·c/λ - Ekin = 6,626·10-34Js·(3·108m/s/4·10-7m) - 1,8·1,602·10-19VAs = 2,0934·10-19J = 1,3eV

Paetec(rot)-LB.S.469 Nr.6

a) Diagramm 

b) abgelesen: h = ∆E/∆f = 0,4·10-14 eVs (Anstieg aus erstem und letztem Wertepaar)   WA=-2,1eV   fG=4,6·1014Hz das entspricht: h = 6,4·10-34Js
b) berechnet:
bulletaus Gleichungssystem  I  1,25eV = h·7,5·1014Hz - WA    und    II  0,17eV = h·5·1014Hz - WA folgt      h = 6,92·10-34Js
bulletaus  WA = h·f - e·U = 6,92·10-34Js·7,5·1014Hz - 1,602·10-19As·1,25V = 3,1875·10-19J = 1,99eV
bulletaus 0 = h·fG - WA   folgt   fG = WA/h = 3,1875·10-19J/6,92·10-34Js = 4,61·1014Hz
c)  aus  ½mv2 = h·f - WA  folgt:

  v = √(2·(h·f - WA)/me) = √(2·(6,92·10-34Js·7,5·1014Hz - 3,1875·10-19J)/9,1·10-31kg) = 6,634·105m/s

Paetec(rot)-LB.S.469 Nr.7

  1. E = h·f = h·c/λ = 6,626·10-34Js·(3·108m/s/3·10-7m) = 6,626·10-19J = 4,14eV

  2. B = P/A = E/(A·t) = (N·h·f)/(A·t) = (N·h·c)/(A·λ·t)       N = (B·A·λ·t)/(h·c) = 3·1014

Paetec(rot)-LB.S.469 Nr.8

           Ekin = h·f - WA = h·c/λ  - WA = 6,626·10-34Js·(3·108m/s/3·10-7m) - 2V·1,602·10-19As = 3,432·10-19J = 2,14eV

Paetec(rot)-LB.S.469 Nr.9

           Ekin = h·f - WA = h·c/λ  - WA = ½·m·v2   v = √(2·(h·c/λ  - WA ))/me) = 8,62·105 m/s

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Das Bohr-Sommerfeldsche Atommodell

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

 

Übungen - Physik   Klasse 13-II GK

        Übung: Der Franck-Hertz-Versuch

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Spektralanalyse

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Laser

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Röntgenstrahlung

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

        Übung: Eigenschaften von Mikroobjekten

Aufgabe:  

        home                        Stoff                            zurück                         HA                               top

 

        Übung: Grundkenntnisse über Atomkerne

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Eigenschaften radioaktiver Strahlung

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Nachweisgeräte für radioaktive Strahlung

 

        home                        Stoff                            zurück                         HA                               top

        Übung: Natürliche Radioaktivität

Aufgabe: Welche Aktivität A besitzt eine 3 μg schweren Probe des Präparates 137Cs?

zu Beginn der Beobachtung:  No = m/mA = m/(A·u) = (3·10-9kg)/(137·1,66·10-27kg) = 1,32·1016

                                        Ao = λ·No = (ln2/T½)·No = (ln2/30a)·1,32·1016 = (ln2/9,46·108s)·1,31·1016 = 9,7 MBq

wegen der großen Halbwertszeit ändert sich diese Aktivität über einen längeren Zeitraum nur unwesentlich

Aufgabe: Wie viel Phosphor (P-32) ist nach 40 Tagen noch aktiv, wenn die ursprüngliche Masse 1g betrug und die Halbwertszeit 14,3 Tage beträgt?

zu Beginn der Beobachtung:  No = m/mA = m/(A·u) = (1·10-3kg)/(32·1,66·10-27kg) = 1,88·1022

                                                N(t) = No·e-(ln2/T½)·t        N(40d) = 1,88·1022 · e-(ln2/14,3d)·40d = 2,71·1021

                                m(40d) = N(40d)·mA = N(40d)·(A·u) = 2,71·1021·(32·1,66·10-27kg) = 1,44·10-4kg = 0,144 g

oder besser:  m(t) = mo·e-(ln2/T½)·t        m(40d) = 1g · e-(ln2/14,3d)·40d = 0,144 g

Aufgabe: Nach wie vielen Halbwertszeiten beträgt die Aktivität eines radioaktiven Präparates nur noch 1% ihres Anfangswertes?

A(t) = Ao·e-(ln2/T½)·t     1/100·Ao = Ao·e-(ln2/T½)·t    1/100 = e-(ln2/T½)·t    ln(1/100) = -(ln2/T½)·t   

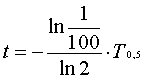
nach ca. 6,64 Halbwertszeiten ist die Aktivität des Präparates auf 1% seines Anfangswertes zurückgegangen.

Aufgabe: Wie viele Betateilchen (Elektronen) werden je Sekunde von einem Gramm Co-60 (Halbwertszeit beträgt 5,3 Jahre) emittiert?

No = m/mA = m/(A·u) = (1·10-3kg)/(60·1,66·10-27kg) = 1,004016064·1022

N(t) = No·e-(ln2/T½)·t        

N(1s) = 1,004016064·1022 · e-(ln2/5,3a)·1s = 1,004016064·1022 · e-(ln2/167140800s)·1s = 1,00401606·1022

∆N = No-N(1s) = 1,004016064·1022 - 1,00401606·1022 = 4,16·1013 und da pro umgewandeltem Kern auch genau ein Betateilchen emittiert wird, ist das gleichzeitig auch die Aktivität des Präparates in Bq

        home                        Stoff                            zurück                         HA                               top